题目内容
已知圆O1和圆O2的极坐标方程分别为ρ=2,ρ2-2| 2 |
| π |
| 4 |
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程.
分析:(1)先利用三角函数的差角公式展开圆O2的极坐标方程的右式,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得圆O2的直角坐标方程及圆O1直角坐标方程.
(2)先在直角坐标系中算出经过两圆交点的直线方程,再利用直角坐标与极坐标间的关系求出其极坐标方程即可.
(2)先在直角坐标系中算出经过两圆交点的直线方程,再利用直角坐标与极坐标间的关系求出其极坐标方程即可.
解答:解:(1)ρ=2?ρ2=4,所以x2+y2=4;因为ρ2-2
ρcos(θ-
)=2,
所以ρ2-2
ρ(cosθcos
+sinθsin
)=2,所以x2+y2-2x-2y-2=0.(5分)
(2)将两圆的直角坐标方程相减,得经过两圆交点的直线方程为x+y=1.
化为极坐标方程为ρcosθ+ρsinθ=1,即ρsin(θ+
)=
.(10分)
| 2 |
| π |
| 4 |
所以ρ2-2
| 2 |
| π |
| 4 |
| π |
| 4 |
(2)将两圆的直角坐标方程相减,得经过两圆交点的直线方程为x+y=1.
化为极坐标方程为ρcosθ+ρsinθ=1,即ρsin(θ+
| π |
| 4 |
| ||
| 2 |
点评:本题考查点的极坐标和直角坐标的互化,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
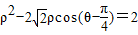 .
.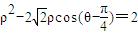 .
. .
.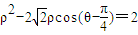 .
.