题目内容
若平面向量 与向量
与向量 的夹角是180°,且
的夹角是180°,且 ,则
,则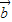 = .
= .
【答案】分析:根据两个向量的夹角是180°,设出要求的向量的坐标,根据向量的模长.利用模长公式求出未知数的值.
解答:解:∵平面向量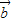 与向量
与向量 的夹角是180°
的夹角是180°
∴平面向量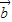 =λ(1,-2)
=λ(1,-2)
∵
∴λ2+4λ2=45
∴λ=±3
∵两个向量的夹角是180°,
∴λ=-3
∴ =(-3,6)
=(-3,6)
故答案为:(-3,6)
点评:本题考查平面向量的坐标运算,本题解题的关键是设出向量的坐标,根据两个向量的方向相反设出结果,注意把不合题意的舍去.
解答:解:∵平面向量
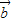 与向量
与向量 的夹角是180°
的夹角是180°∴平面向量
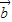 =λ(1,-2)
=λ(1,-2)∵

∴λ2+4λ2=45
∴λ=±3
∵两个向量的夹角是180°,
∴λ=-3
∴
 =(-3,6)
=(-3,6)故答案为:(-3,6)
点评:本题考查平面向量的坐标运算,本题解题的关键是设出向量的坐标,根据两个向量的方向相反设出结果,注意把不合题意的舍去.

练习册系列答案
相关题目