题目内容
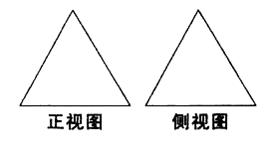
已知一个棱长为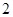 的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的体积是
的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的体积是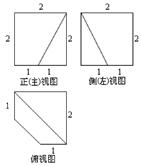
| A.8 | B.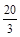 |
C.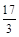 | D.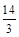 |
C
解析试题分析:根据三视图可知,该几何体是由一个正方体被平面截去一个三棱台得到的几何体,该三棱台的体积为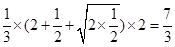 ,所以该几何体的体积为
,所以该几何体的体积为
考点:本题考查三视图的概念与几何体体积的计算,考查空间想象能力,较难题.
点评:解决与三视图有关的问题,首先要根据三视图正确还原几何体,需要学生有较强的空间想象能力.

练习册系列答案
相关题目
下列说法中正确的是
| A.棱柱的侧面可以是三角形 |
| B.正方体和长方体都是特殊的四棱柱 |
| C.所有的几何体的表面都能展成平面图形 |
| D.棱柱的各条棱都相等 |
某几何体的三视图如图所示,其中三角形的三边长与圆的直径均为2,则该几何体的体积为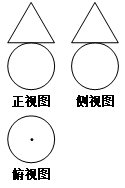
A.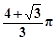 | B.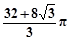 |
C.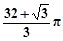 | D.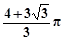 |
已知几何体M的正视图是一个面积为2 的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为
的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为
A.6 和 和  | B.6 +4 +4 和 和  |
C.6 +4 +4 和 和  | D.4( + + )和 )和  |
如图是某几何体的三视图,则该几何体的体积为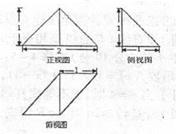
| A.1 | B.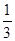 | C. | D.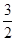 |
某空间几何体的三视图及尺寸如图1,则该几何体的体积是
A. | B. | C. | D. |
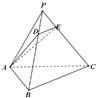
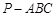 的底面是正三角形,各条侧棱均相等,
的底面是正三角形,各条侧棱均相等,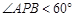 .设点
.设点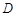 、
、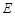 分别在线段
分别在线段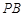 、
、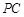 上,且
上,且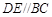 ,记
,记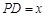 ,
,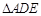 周长为
周长为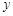 ,则
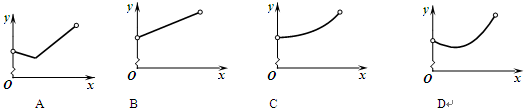
,则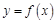 的图象可能是
的图象可能是