题目内容
若正六棱锥的底面边长为3cm,侧面积是底面积的
倍,则这个棱锥的高是
cm.
| 3 |
| 3 |
| 2 |
| 6 |
| 3 |
| 2 |
| 6 |
分析:由已知中正六棱锥的全面积是底面积的
倍,得到其侧高与底面中心到对称棱的距离之间为
:1,构造直角三角形PQO(其中P为棱锥的顶点,Q为底面棱的中点,O为底面的中心),解三角形即可得到侧面与底面所成的角,最后利用直角三角形求出棱锥的高.
| 3 |
| 3 |
解答:解: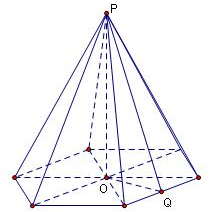 由于正六棱锥的全面积是底面积的3倍,
由于正六棱锥的全面积是底面积的3倍,
不妨令P为棱锥的顶点,Q为底面棱的中点,O为底面的中心
∵侧面积是底面积的3倍,则PQ=3OQ
则∠PQO即为侧面与底面所成的角
∵cos∠PQO=
,∴sin∠PQO=
,
∴tan∠PQO=
,
在直角三角PQO中,PO=QO•tan∠PQO=
×3×
=
故答案为:
.
 由于正六棱锥的全面积是底面积的3倍,
由于正六棱锥的全面积是底面积的3倍,不妨令P为棱锥的顶点,Q为底面棱的中点,O为底面的中心
∵侧面积是底面积的3倍,则PQ=3OQ
则∠PQO即为侧面与底面所成的角
∵cos∠PQO=
| ||
| 3 |
| ||
| 3 |
∴tan∠PQO=
| 2 |
在直角三角PQO中,PO=QO•tan∠PQO=
| ||
| 2 |
| 2 |
| 3 |
| 2 |
| 6 |
故答案为:
| 3 |
| 2 |
| 6 |
点评:本题考查棱锥的结构特征等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题

练习册系列答案
相关题目
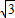 倍,则这个棱锥的高是 cm.
倍,则这个棱锥的高是 cm. ,则它的侧面与底面所成的二面角的大小为 °.
,则它的侧面与底面所成的二面角的大小为 °.