题目内容
已知圆C(圆心为原点)与直线l,从l与C上各取2个点,将其坐标记录于下表中:
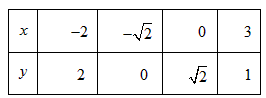
(1)求圆C与直线l的方程;
(2)设表中直线l上的两个点为A,B,试探究在圆C上是否存在点P,使得|PA|=|PB|?若不存在请说明理由,若存在,请指出共有几个这样的点(不必具体求出这些点的坐标)。
(2)设表中直线l上的两个点为A,B,试探究在圆C上是否存在点P,使得|PA|=|PB|?若不存在请说明理由,若存在,请指出共有几个这样的点(不必具体求出这些点的坐标)。
解:(1)因为圆上的点必满足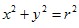 ,故只能是
,故只能是 在圆上,
在圆上,
得圆C方程为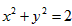 ;
;
则(-2,2),(3,1)在直线上,易得直线的方程为x+5y-8=0;
(2)不妨设l上两点为A(-2,2),B(3,1),设P(x,y),易得线段AB的垂直平分线方程为5x-y-1=0,
由点到直线的距离公式可得圆心到该直线的距离为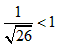 ,故该直线与圆有2个不同交点,这两个点都满足|PA|=|PB|;
,故该直线与圆有2个不同交点,这两个点都满足|PA|=|PB|;
综上可知存在2个点使得|PA|=|PB。
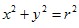 ,故只能是
,故只能是 在圆上,
在圆上,得圆C方程为
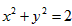 ;
;则(-2,2),(3,1)在直线上,易得直线的方程为x+5y-8=0;
(2)不妨设l上两点为A(-2,2),B(3,1),设P(x,y),易得线段AB的垂直平分线方程为5x-y-1=0,
由点到直线的距离公式可得圆心到该直线的距离为
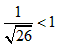 ,故该直线与圆有2个不同交点,这两个点都满足|PA|=|PB|;
,故该直线与圆有2个不同交点,这两个点都满足|PA|=|PB|;综上可知存在2个点使得|PA|=|PB。

练习册系列答案
相关题目
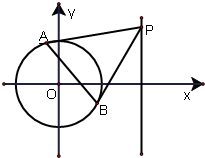 已知圆C的圆心为原点O,且与直线
已知圆C的圆心为原点O,且与直线 =0相切.
=0相切.
 相切.
相切.
 相切.
相切.