题目内容
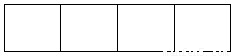
 用3种不同的颜色给4个矩形随机涂色,每个矩形只涂一种颜色,且相邻的不能涂同一个颜色
用3种不同的颜色给4个矩形随机涂色,每个矩形只涂一种颜色,且相邻的不能涂同一个颜色求:
(1)只用了两种颜色的概率;
(2)三种颜色都用了的概率.
分析:由题意,涂色方式共24种,两大类:第一类只用2种颜色,共有方法2
=6种;第二类只用3种颜色,共有方法24-6=18种.由古典概型可得.
| C | 2 3 |
解答:解:由题意,涂色方式共两大类:
由分步计数原理可得,共3×2×2×2=24种,
第一类只用2种颜色,共有方法2
=6种;
第二类只用3种颜色,共有方法24-6=18种.
故(1)只用了两种颜色的概率为:
=
;
(2)三种颜色都用了的概率为:
=
由分步计数原理可得,共3×2×2×2=24种,
第一类只用2种颜色,共有方法2
| C | 2 3 |
第二类只用3种颜色,共有方法24-6=18种.
故(1)只用了两种颜色的概率为:
| 6 |
| 24 |
| 1 |
| 4 |
(2)三种颜色都用了的概率为:
| 18 |
| 26 |
| 3 |
| 4 |
点评:本题为古典概型的求解,求出符合条件的基本事件数是解决问题的关键,属基础题.

练习册系列答案
相关题目
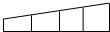 15、如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色.要求最多使用3种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有
15、如图,用6种不同的颜色给图中的4个格子涂色,每个格子涂一种颜色.要求最多使用3种颜色且相邻的两个格子颜色不同,则不同的涂色方法共有 用3种不同的颜色给4个矩形随机涂色,每个矩形只涂一种颜色,且相邻的不能涂同一个颜色
用3种不同的颜色给4个矩形随机涂色,每个矩形只涂一种颜色,且相邻的不能涂同一个颜色