题目内容
(I)已知a1,a2∈R,a1+a2=1,求证:a12+a22≥| 1 |
| 2 |
(II)若a1,a2,…an∈R,a1+a2+…+an=1,求证:a12+a22+…+an2≥
| 1 |
| n |
分析:(I)构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2x+a12+a22,因为对一切x∈R,恒有f(x)≥0,所以△≤0,从而得结论;
(II)由已知中已知a1,a2∈R,a1+a2=1,求证a12+a22 ≥
,及整个式子的证明过程,我们根据归纳推理可以得到一个一般性的公式,若a1,a2,…,an∈R,a1+a2+…+an=1,则a12+a22+…+an2≥
,但此公式是由归纳推理得到的,其正确性还没有得到验证,观察已知中的证明过程,我们可以类比对此公式进行证明.
(II)由已知中已知a1,a2∈R,a1+a2=1,求证a12+a22 ≥
| 1 |
| 2 |
| 1 |
| n |
解答:(I)证明:构造函数f(x)=(x-a1)2+(x-a2)2=2x2-2x+a12+a22
因为对一切x∈R,恒有f(x)≥0,
所以△=4-8(a12+a22)≤0,从而得a12+a22 ≥
,
(II)证明:构造函数
f(x)=(x-a1)2+(x-a2)2+…+(x-an)2
=nx2-2(a1+a2+…+an)x+a12+a22+…+an2
=2x2-2x+a12+a22+…+an2
因为对一切x∈R,都有f(x)≥0,所以△=4-4n(a12+a22+…+an2)≤0
从而证得:a12+a22+…+an2≥
因为对一切x∈R,恒有f(x)≥0,
所以△=4-8(a12+a22)≤0,从而得a12+a22 ≥
| 1 |
| 2 |
(II)证明:构造函数
f(x)=(x-a1)2+(x-a2)2+…+(x-an)2
=nx2-2(a1+a2+…+an)x+a12+a22+…+an2
=2x2-2x+a12+a22+…+an2
因为对一切x∈R,都有f(x)≥0,所以△=4-4n(a12+a22+…+an2)≤0
从而证得:a12+a22+…+an2≥
| 1 |
| n |
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).(3)对归纳得到的一般性结论进行证明.

练习册系列答案
相关题目
 ;
; .
. ;
;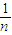 .
. ;
;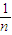 .
.