题目内容
为了了解一个小水库中养殖的鱼有关情况,从这个水库中多个不同位置捕捞出100条鱼,称得每条鱼的质量(单位:千克),并将所得数据分组,画出频率分布直方图(如图所示)
(Ⅰ)在答题卡上的表格中填写相应的频率;
(Ⅱ)估计数据落在(1.15,1.30)中的概率为多少;
(Ⅲ)将上面捕捞的100条鱼分别作一记号后再放回水库,几天后再从水库的多处不同位置捕捞出120条鱼,其中带有记号的鱼有6条,请根据这一情况来估计该水库中鱼的总条数。
解:(Ⅰ)根据频率分布直方图可知,频率=组距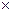 (频率/组距),故可得下表
(频率/组距),故可得下表
(Ⅱ)0.30+0.15+0.02=0.47,所以数据落在分组 频率 
0.05 
0.20 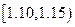
0.28 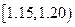
0.30 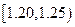
0.15 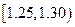
0.02 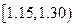 中的概率约为0.47.
中的概率约为0.47.
(Ⅲ)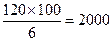 ,所以水库中鱼的总条数约为2000条.
,所以水库中鱼的总条数约为2000条.
解析

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
(本题满分12分)某农科所对冬季昼夜温差与某反季节大豆种子发芽多少之间的关系进行分析研究,他们记录了12月1日至5日的昼夜温差与每天100颗种子的发芽数,数据如下表:
| 日 期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差 (0C) (0C) | 10 | 11 | 13 | 12 | 8 |
发芽数 (颗) (颗) | 23 | 25 | 30 | 26 | 16 |
(1) 若先选取的是12月1日和5日的数据,请根据2日至4日的三组数据,求
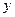 关于
关于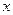 的线性回归方程
的线性回归方程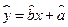 ;
; (2) 若由回归方程得到的估计数据与检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试判断(1)中所得的线性回归方程是否可靠?说明理由.
(10分)假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:若由资料知,y对x呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
| x | 2 | 3 | 4 | 5 | 6 |
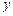 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下: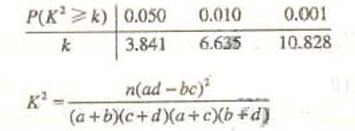
| 是否需要志愿 性别 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
(2) 能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3) 根据(2)的结论,能否提供更好的调查方法来估计该地区老年人,需要志愿帮助的老年人的比例?说明理由
附:
(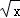 +
+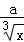 )5展开式的常数项为80,则a的值为( )
)5展开式的常数项为80,则a的值为( )
| A.1 | B.2 | C.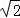 | D.4 |
设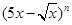 的展开式的各项系数之和为M,二项式系数之和为N,若M
的展开式的各项系数之和为M,二项式系数之和为N,若M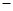 N=240,则展开式中
N=240,则展开式中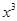 的系数为( )
的系数为( )
| A.-150 | B.150 | C.-560 | D.560 |
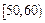 ,第二组
,第二组 ,…,第五组
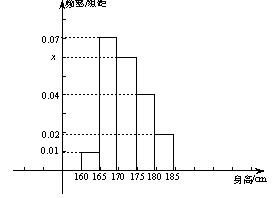
,…,第五组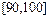 .下图是按上述分组方法得到的频率分布直方图。
.下图是按上述分组方法得到的频率分布直方图。
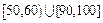 内的所有学生中随机抽取两名同学,设其测试成绩分别为
内的所有学生中随机抽取两名同学,设其测试成绩分别为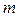 ,
,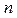 ,求事件“
,求事件“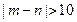 ”概率.
”概率.
 ;
; 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量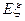 .(要求:答案用最简分数表示)
.(要求:答案用最简分数表示)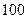 名学生,测得他们的身高(单位:
名学生,测得他们的身高(单位: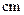 ),按照区间
),按照区间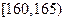 ,
,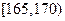 ,
,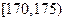 ,
,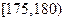 ,
,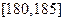 分组,得到样本身高的频率分布直方图(如图).
分组,得到样本身高的频率分布直方图(如图).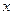 的值及身高在
的值及身高在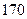
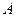 ,
,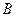 ,
,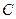 三个组,用分层抽样的方法从三个组中抽取
三个组,用分层抽样的方法从三个组中抽取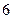 人,求从这三个组分别抽取的学生人数;
人,求从这三个组分别抽取的学生人数;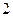 人,用列举法计算
人,用列举法计算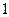 人被抽中的概率.
人被抽中的概率.