题目内容
 我们把离心率为e=
我们把离心率为e=
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
①双曲线x2-
| 2y2 | ||
|
②若b2=ac,则该双曲线是黄金曲线;
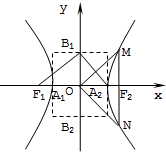
③若∠F1B1A2=900,则该双曲线是黄金曲线;
④若∠MON=90°,则该双曲线是黄金曲线;
其中正确的是
①②③④
①②③④
.分析:对于①求出双曲线的离心率判断正误;
对于②通过a,b,c的关系,求出双曲线的离心率判断正误;
对于③通过∠F1B1A2=90°,转化为a,b,c的关系,求出双曲线的离心率判断正误;
对于④利用∠MON=90°,转化为a,b,c的关系,求出双曲线的离心率判断正误;
对于②通过a,b,c的关系,求出双曲线的离心率判断正误;
对于③通过∠F1B1A2=90°,转化为a,b,c的关系,求出双曲线的离心率判断正误;
对于④利用∠MON=90°,转化为a,b,c的关系,求出双曲线的离心率判断正误;
解答:解:①双曲线x2-
=1可知,a=1,b2=
,所以c2=
,
所以双曲线的离心率为
=
,是黄金曲线,正确;
②b2=ac,即-a2+c2=ac,解得e=
=
则该双曲线是黄金曲线;正确.
③因为∠F1B1A2=90°,所以(a+c)2=a2+2b2+c2,即-a2+c2=ac,解得e=
=
则该双曲线是黄金曲线;正确.
④因为∠MON=90°,所以c=
,即a2+c2=ac,解得e=
=
则该双曲线是黄金曲线;正确.
故答案为:①②③④
| 2y2 | ||
|
| ||
| 2 |
| ||
| 2 |
所以双曲线的离心率为
| ||||||
| 1 |
| ||
| 2 |
②b2=ac,即-a2+c2=ac,解得e=
| c |
| a |
| ||
| 2 |
③因为∠F1B1A2=90°,所以(a+c)2=a2+2b2+c2,即-a2+c2=ac,解得e=
| c |
| a |
| ||
| 2 |
④因为∠MON=90°,所以c=
| b2 |
| a |
| c |
| a |
| ||
| 2 |
故答案为:①②③④
点评:本题考查双曲线的基本性质,a,b,c的关系,离心率的求法,考查计算能力.

练习册系列答案
相关题目
 我们把离心率为e=
我们把离心率为e=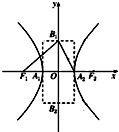 我们把离心率为e=
我们把离心率为e=