Question

在棱长为a的正方体盒内装有五个球，其中四个是半径为r的等球，放在盒底四角，另一个大球半径为R，放在四个等球的上面.若四个等球相邻两个外切，且还与正方体的侧面及下底面相切，而这个大球分别与这四个等球相切，且与上底面相切，试用a表示R、r.

Answer 1

解析：提炼球心，构造正四棱锥，寻找a、R、r的数量关系.依题意，得r=a.

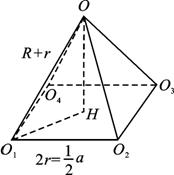
如图，将五个球的球心提炼出来，构成正四棱锥O-O₁O₂O₃O₄，

其底面正方形的边长2r=a，侧棱长为R+r=R+a.正四棱锥的高

OH==.

∵R+OH+r=a,∴R++=a，即-R.

两边平方，化简得R=a.

∴所求的表达式为r=a，R=a.