题目内容
判断正误:已知抛物线的对称轴为y轴, 顶点的坐标为(0,-1), 并且抛物线在x轴上截得的弦BC(B为左交点)的长为2, 在此抛物线上取两点P(异于B), Q, 若BP⊥PQ, 那么点Q存在时, 点Q的横坐标满足x∈(-∞,-3)∪(1,+∞).
( )
答案:F
解析:
解析:
|
解: 抛物线方程为y=x2-1 设P(x0,x02-1) (x0≠-1) Q(x, x2-1)(x≠x0,x≠-1)
从而得x02+(x-1)x0+(1-x)=0(x0≠-1) ∵x0∈R, ∴ △=(x-1)2+4(x-1)≥0 得x≥1或x≤-3 ∴点Q在抛物线y=x2-1上且满足 x∈(-∞,-3]U[1,+∞)的点
|

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 =-1
=-1
 的焦点与椭圆
的焦点与椭圆 的右焦点重合.(Ⅰ)求抛物线
的右焦点重合.(Ⅰ)求抛物线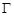 的方程;
的方程; 恒过点
恒过点 与抛物线
与抛物线 轴交于C点,请你观察并判断:在线段MA,MB,MC,AB中,哪三条线段的长总能构成等比数列?说明你的结论并给出证明.
轴交于C点,请你观察并判断:在线段MA,MB,MC,AB中,哪三条线段的长总能构成等比数列?说明你的结论并给出证明.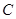 的方程 为
的方程 为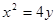 ,直线
,直线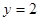 与抛物线
与抛物线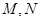 两点,点
两点,点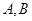 在抛物线
在抛物线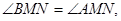 求证:直线
求证:直线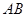
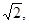 且点
且点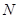 到 直线
到 直线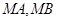 的距离的和为
的距离的和为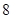 ,试判断
,试判断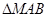 的形状,并证明你的结论.
的形状,并证明你的结论. (Ⅱ)若直线
(Ⅱ)若直线