题目内容
写出下列函数的单调增区间:
(1)y=3sin(2x-![]() );(2)y=2cos(2x+
);(2)y=2cos(2x+![]() );(3)y=logi[sin(2x+
);(3)y=logi[sin(2x+![]() )].
)].
解析:
|
思路分析:应用正、余弦函数的单调性.(1)设z=2x- 解:(1)设z=2x- 即2x- 由- 得- 即- 所以,函数y=3sin(2x- (2)由-π+2kπ≤2x+ 即- 所以,函数y=2cos(2x+ (3)设u=sin(2x+ 由y=sinx(y>0)的图象,可知y=sinx(y>0)的增区间为(2kπ,2kπ+ 2kπ<2x+ 所以- 所以,函数y=log2[sin(2x+ 方法归纳:本题的关键在于转化思想的应用,使用了整体换元法.函数的单调性是函数在定义域内的某个区间上的性质,因此,要求函数的单调区间,应首先求函数的定义域.此外,函数的单调区间应写成区间的形式. |

 培优三好生系列答案
培优三好生系列答案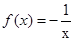 的单调增区间是(-∞,0)
的单调增区间是(-∞,0)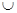 (0,+∞)
(0,+∞)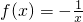 的单调增区间是(-∞,0)∪(0,+∞)
的单调增区间是(-∞,0)∪(0,+∞)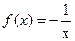 的单调增区间是(-∞,0)
的单调增区间是(-∞,0) (0,+∞)
(0,+∞)