题目内容
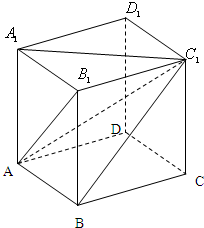 在平行六面体ABCD-A1B1C1D1中,A1A⊥面ABCD,AB1⊥BC1,AB=CC1=3,BC=5.
在平行六面体ABCD-A1B1C1D1中,A1A⊥面ABCD,AB1⊥BC1,AB=CC1=3,BC=5.(Ⅰ)求证:A1C1⊥AB;
(Ⅱ)求点B1到平面ABC1的距离.
分析:(Ⅰ)连接A1B,由AB=CC1,知AB=BB1,由AA1⊥面ABCD,知AA1⊥AB.所以四边形ABB1A1为正方形.由此能够证明A1C1⊥AB.
(Ⅱ)由A1B1∥AB,知A1B1∥面ABC1.则A1到平面ABC1的距离即为B1到平面ABC1的距离.由AB⊥A1A,AB⊥A1C1,知AB⊥面AA1C1C,面ABC1⊥面AA1C1C.过A1作A1G⊥AC1于G,则A1G⊥面ABC1,则 A1G的长就是点A1到平面ABC1的距离.由此能求出点B1到平面ABC1的距离.
(Ⅱ)由A1B1∥AB,知A1B1∥面ABC1.则A1到平面ABC1的距离即为B1到平面ABC1的距离.由AB⊥A1A,AB⊥A1C1,知AB⊥面AA1C1C,面ABC1⊥面AA1C1C.过A1作A1G⊥AC1于G,则A1G⊥面ABC1,则 A1G的长就是点A1到平面ABC1的距离.由此能求出点B1到平面ABC1的距离.
解答:解:(Ⅰ)证明:连接A1B,∵AB=CC1∴AB=BB1
又AA1⊥面ABCD∴AA1⊥AB
则四边形ABB1A1为正方形.∴AB1⊥A1B.∵AB1⊥BC1,∴AB1⊥面A1BC1.∴AB1⊥A1C1,∵BB1⊥A1C1,∴A1C1⊥面A1ABB1,∴A1C1⊥AB
(Ⅱ)∵A1B1∥AB,∴A1B1∥面ABC1.
则A1到平面ABC1的距离即为B1到平面ABC1的距离.
由( I)知,AB⊥A1A,AB⊥A1C1,∴AB⊥面AA1C1C,∴面ABC1⊥面AA1C1C.
过A1作A1G⊥AC1于G,则A1G⊥面ABC1,
则 A1G的长就是点A1到平面ABC1的距离.
在Rt△A1B1C1中,A1C12=B1C12-A1B12=52-32=16,A1C1=4,
在Rt△A1AC1中,AC12=A1C12+A1A2=42+32=25,AC1=5.
则由AC1•A1G=AA1•A1C1可得 5×A1G=3×4,∴A1G=
故 所求距离为
.
又AA1⊥面ABCD∴AA1⊥AB
则四边形ABB1A1为正方形.∴AB1⊥A1B.∵AB1⊥BC1,∴AB1⊥面A1BC1.∴AB1⊥A1C1,∵BB1⊥A1C1,∴A1C1⊥面A1ABB1,∴A1C1⊥AB
(Ⅱ)∵A1B1∥AB,∴A1B1∥面ABC1.
则A1到平面ABC1的距离即为B1到平面ABC1的距离.
由( I)知,AB⊥A1A,AB⊥A1C1,∴AB⊥面AA1C1C,∴面ABC1⊥面AA1C1C.
过A1作A1G⊥AC1于G,则A1G⊥面ABC1,
则 A1G的长就是点A1到平面ABC1的距离.
在Rt△A1B1C1中,A1C12=B1C12-A1B12=52-32=16,A1C1=4,
在Rt△A1AC1中,AC12=A1C12+A1A2=42+32=25,AC1=5.
则由AC1•A1G=AA1•A1C1可得 5×A1G=3×4,∴A1G=
| 12 |
| 5 |
故 所求距离为
| 12 |
| 5 |
点评:本题考查点、线、面间距离的计算,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
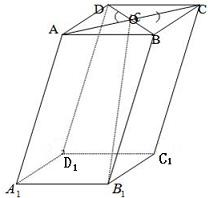
如图,在平行六面体ABCD-A1B1C1D1中,O为AC与BD的交点,若
=
,
=
,
=
,则向量
等于( )
| A1B1 |
| a |
| A1D1 |
| b |
| AA1 |
| c |
| B1O |

A、
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、-
|
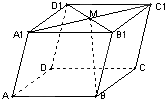 如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若
如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| BM |
A、-
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、
|
 已知在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,且∠BAD=∠BAA1=∠DAA1=60°,求AC1的长.
已知在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,且∠BAD=∠BAA1=∠DAA1=60°,求AC1的长.