题目内容
【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2﹣2x.
(1)求f(x)的解析式,并画出的f(x)图象; 
(2)设g(x)=f(x)﹣k,利用图象讨论:当实数k为何值时,函数g(x)有一个零点?二个零点?三个零点?
【答案】
(1)解:当x≥0时,f(x)=x2﹣2x.
设x<0可得﹣x>0,则f(﹣x)=(﹣x)2﹣2(﹣x)=x2+2x
∵函数f(x)为奇函数,则f(x)=﹣f(﹣x)=﹣x2﹣2x
∴ ![]() 函数的图象如图所示
函数的图象如图所示
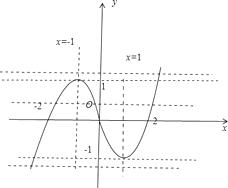
(2)解:由g(x)=f(x)﹣k=0可得f(x)=k
结合函数的图象可知
①当k<﹣1或k>1时,y=k与y=f(x)的图象有1个交点,即g(x)=f(x)﹣k有1个零点
②当k=﹣1或k=1时,y=k与y=f(x)有2个交点,即g(x)=f(x)﹣k有2个零点
③当﹣1<k<1时,y=k与y=f(x)有3个交点,即g(x)=f(x)﹣k有3个零点
【解析】(1)先设x<0可得﹣x>0,则f(﹣x)=(﹣x)2﹣2(﹣x)=x2+2x,由函数f(x)为奇函数可得f(x)=﹣f(﹣x),可求,结合二次函数的图象可作出f(x)的图象;(2)由g(x)=f(x)﹣k=0可得f(x)=k,结合函数的图象可,要求g(x)=f(x)﹣k的零点个数,只要结合函数的图象,判断y=f(x)与y=k的交点个数
【考点精析】利用函数奇偶性的性质对题目进行判断即可得到答案,需要熟知在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
