题目内容
定义在区间[0,
]上的函数y=Asin2ωx(A>0)与直线y=2有且只有一个公共点,且截直线y=1所得的弦长为2,则ω=
.
| π |
| ω |
| π |
| 6 |
| π |
| 6 |
分析:可设出直线y=1与函数y=2sin2ωx在区间[0,
]上的交点为M(x1,
),N(x2,
),再根据题意得出x2-x1=2,2ωx2=
,2ωx1=
,问题即可解决.
| π |
| ω |
| 1 |
| 2 |
| 1 |
| 2 |
| 5π |
| 6 |
| π |
| 6 |
解答:解:由题意可得A=2,设直线y=1与函数y=2sin2ωx在区间[0,
]上的交点为M(x1,
),N(x2,
),
则x2-x1=2;
∵sin2ωx=
,x∈[0,
],
∴2ωx2=
,2ωx1=
,
∴2ωx2-2ωx1=2ω(x2-x1)=4ω=
,
∴ω=
.
故答案为:
.
| π |
| ω |
| 1 |
| 2 |
| 1 |
| 2 |
则x2-x1=2;
∵sin2ωx=
| 1 |
| 2 |
| π |
| ω |
∴2ωx2=
| 5π |
| 6 |
| π |
| 6 |
∴2ωx2-2ωx1=2ω(x2-x1)=4ω=
| 2π |
| 3 |
∴ω=
| π |
| 6 |
故答案为:
| π |
| 6 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,难点在于设出交点为M(x1,
),N(x2,
)后,结论2ωx2=
,2ωx1=
的分析与应用,属于中档题.
| 1 |
| 2 |
| 1 |
| 2 |
| 5π |
| 6 |
| π |
| 6 |

练习册系列答案
相关题目
 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1、x2,给出下列结论:
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1、x2,给出下列结论: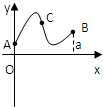 定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为S(x),则函数S(x)的导函数S′(x)的图象大致是( )
定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为S(x),则函数S(x)的导函数S′(x)的图象大致是( )