Question

若A、B是抛物线y²=4x上的不同两点，弦AB（不平行于y轴）的垂直平分线与x轴相交于点P，则称弦AB是点P的一条“相关弦”．已知当x>2时，点P（x,0）存在无穷多条“相关弦”．给定x₀>2．

（I）证明：点P（x₀,0）的所有“相关弦”的中点的横坐标相同；

（II）试问：点P（x₀,0）的“相关弦”的弦长中是否存在最大值？若存在，求其最大值（用x₀表示）：若不存在，请说明理由．

Answer 1

解:（I）设AB为点P（x₀,0）的任意一条“相关弦”，且点A、B的坐标分别是

（x₁,y₁）、（x₂,y₂）（x₁x₂）,则y²₁=4x_1, y²₂=4x₂,

两式相减得（y₁+y₂）（y₁-y₂）=4（x₁-x₂）．因为x₁x₂,所以y₁+y₂0．

设直线AB的斜率是k，弦AB的中点是M（x_m, y_m）,则

k=．

从而AB的垂直平分线l的方程为

又点P（x₀,0）在直线l上，所以

而于是

故点P（x₀,0）的所有“相关弦”的中点的横坐标都是x₀-2．

（Ⅱ）由（Ⅰ）知，弦AB所在直线的方程是，代入中，

整理得     (1)

则是方程（1）的两个实根，且

设点P的“相关弦”AB的弦长为l，则

 

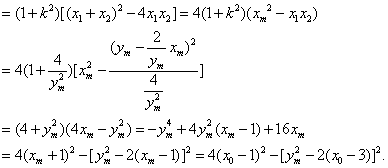
因为0<<4x_m=4（x₀-2） =4x₀-8,于是设t=,则t（0,4x₀-8）．

记l²=g（t）=-[t-2（x₀-3）]²+4（x₀-1）²

若x₀>3,则2（x₀-3）（0, 4x₀-8）,所以当t=2（x₀-3）,即=2（x₀-3）时,

l有最大值2（x₀-1）．

若2<x₀≤3,则2（x₀-1）0,   g（t）在区间（0，4 x₀-8）上是减函数，所以

0<l²<16（x₀-2）,l不存在最大值．

综上所述，当x₀>3时，点P（x₀,0）的“相关弦”的弦长中存在最大值，且最大值为

2（x₀-1）；当2< x₀3时，点P（x₀,0）的“相关弦”的弦长中不存在最大值．