题目内容
求下列函数的单调区间,并指出其增减性.
(1)y=a1-x2(a>0且a≠1);
(2)y=log
(4x-x3).
(1)y=a1-x2(a>0且a≠1);
(2)y=log
| 1 | 2 |
分析:(1)对底数a分0<a<1和a>1两种情况讨论,根据y=ax和y=1-x2两个函数的单调性,即可求出复合函数y=a1-x2(a>0且a≠1)的单调区间及单调性;
(2)先求出函数的定义域,根据对数函数的底数为
,确定外函数为单调减函数,内函数为y=4x-x3,利用导数大于0和导数小于0,分别确定出内函数的单调性,最后即可求出复合函数y=log
(4x-x3)的单调区间及单调性.
(2)先求出函数的定义域,根据对数函数的底数为
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)令t=1-x2,则y=at,
①当a>1时,y=at在R上为单调递增函数,而t=1-x2在(-∞,0]上单调递增,在[0,+∞)上单调递减,
∴y=a1-x2在(-∞,0]上单调递增,在[0,+∞)上单调递减;
②当0<a<1时,y=at在R上为单调递减函数,而t=1-x2在(-∞,0]上单调递增,在[0,+∞)上单调递减,
∴y=a1-x2在(-∞,0]上单调递减,在[0,+∞)上单调递增.
综合①②,当a>1时,y=a1-x2在(-∞,0]上单调递增,在[0,+∞)上单调递减;
当0<a<1时,y=a1-x2在(-∞,0]上单调递减,在[0,+∞)上单调递增.
(2)∵y=log
(4x-x3),要使函数有意义,则4x-x3>0,解得,x<-2或0<x<2,
∴y=log
(4x-x3)的定义域为(-∞,-2)∪(0,2).
令g(x)=4x-x3,g′(x)=-3x2+4,
令g′(x)=-3x2+4>0,解得,-
<x<
,
令g′(x)=-3x2+4<0,解得,x<-
或x>
,
∴g(x)=4x-x3在(-
,
)上单调递增,在(-∞,-
)∪(
,+∞)上单调递减,
y=log
x在(0,+∞)上单调递减,结合函数y=log
(4x-x3)的定义域为(-∞,-2)∪(0,2),
∴函数y=log
(4x-x3)在(0,
)上单调递减,在(-∞,-2)和(
,2)上单调递增.
①当a>1时,y=at在R上为单调递增函数,而t=1-x2在(-∞,0]上单调递增,在[0,+∞)上单调递减,
∴y=a1-x2在(-∞,0]上单调递增,在[0,+∞)上单调递减;
②当0<a<1时,y=at在R上为单调递减函数,而t=1-x2在(-∞,0]上单调递增,在[0,+∞)上单调递减,
∴y=a1-x2在(-∞,0]上单调递减,在[0,+∞)上单调递增.
综合①②,当a>1时,y=a1-x2在(-∞,0]上单调递增,在[0,+∞)上单调递减;
当0<a<1时,y=a1-x2在(-∞,0]上单调递减,在[0,+∞)上单调递增.
(2)∵y=log
| 1 |
| 2 |
∴y=log
| 1 |
| 2 |
令g(x)=4x-x3,g′(x)=-3x2+4,
令g′(x)=-3x2+4>0,解得,-
2
| ||
| 3 |
2
| ||
| 3 |
令g′(x)=-3x2+4<0,解得,x<-
2
| ||
| 3 |
2
| ||
| 3 |
∴g(x)=4x-x3在(-
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
y=log
| 1 |
| 2 |
| 1 |
| 2 |
∴函数y=log
| 1 |
| 2 |
2
| ||
| 3 |
2
| ||
| 3 |
点评:本题考查了复合函数的单调性,复合函数分别以指数函数和对数函数为背景.对于指数函数和对数函数的单调性与底数的值有关,若底数是参数的话,要注意对参数的分类讨论.另外对于复合函数的单调性要注意把握“同增异减”来判断,求单调区间时要考虑函数的定义域,单调区间是定义域的子集.属于中档题.

练习册系列答案
相关题目
 ; (2)y=
; (2)y= tan2x+1;
tan2x+1;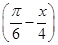 .
.