题目内容
如图2-5-19,已知PA为⊙O的切线,PO交⊙O于点B,BC⊥PA于点C,交⊙O于点D,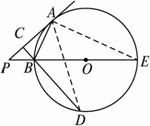
图2-5-19
(1)求证:AB2=PB·BD.
(2)若PA =15,PB =5,求BD的长.
思路分析:(1)只需证△PBA∽△ABD.?
(2)在(1)的基础上,只需求AB,因此寻找AB与BE的关系式,这可以通过相似三角形和勾股定理达到目的.

(1)证明:连结AD,延长PO交⊙O于E,连结AE.?
∵BC⊥PA,∴∠P +∠PBC =90°.?
∵BE为直径,?
∴∠BAE =90°,∠BAD +DAE =90°.?
∵∠DAE =∠DBE =∠PBC,∴∠P =∠BAD.?
又∵∠PAB =∠ADB,∴△PBA∽△ABD.?
∴![]() =
=![]() ,即AB2 =PB·BD.
,即AB2 =PB·BD.
(2)解:∵PA为切线,∴PA2=PB·PE.?
又PA =15,PB =5,∴PE =45.?
∴BE =40.?
∵△PBA∽△PAE,∴![]() =
=![]() =
=![]() =
=![]() .?
.?
设AB =x,则AE =3x.
又AB2+AE2=BE2,?
∴x2+(3x)2=1 600,解得x2=160.?
代入AB2=PB·BD,得BD=32.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,点P到平面α的距离PH=0.4(km).沿山脚原有一段笔直的公路AB可供利用.从点O到山脚修路的造价为a万元/km,原有公路改建费用为
,点P到平面α的距离PH=0.4(km).沿山脚原有一段笔直的公路AB可供利用.从点O到山脚修路的造价为a万元/km,原有公路改建费用为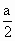 万元/km.当山坡上公路长度为
万元/km.当山坡上公路长度为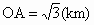 .
.
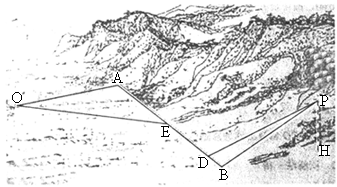
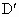 、
、 ,使沿折线
,使沿折线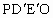 修建公路的总造价小于(2)中得到的最小总造价,证明你的结论.
修建公路的总造价小于(2)中得到的最小总造价,证明你的结论.