题目内容
复数z=cos75o+isin75o (i是虚数单位),则在复平面内z2对应的点位于第__ _象限。
二
本题考查复数的代数形式的乘除法则,考查复数的几何意义,属于基础题.
因为z="cos75°+isin75°" ,所以根据复数的四则运算法则得到,z2=(cos75°+isin75°)2,=cos275°+2isin75°cos75°+(isin75°)2,=cos150°+isin150°= ,故复平面内z2对应的点位于第二象限。
,故复平面内z2对应的点位于第二象限。
解决该试题的关键是利用复数的乘法法则求出z2,根据复数的几何意义求出z2对应的点的坐标,根据坐标判断出点所在的象限.
因为z="cos75°+isin75°" ,所以根据复数的四则运算法则得到,z2=(cos75°+isin75°)2,=cos275°+2isin75°cos75°+(isin75°)2,=cos150°+isin150°=
 ,故复平面内z2对应的点位于第二象限。
,故复平面内z2对应的点位于第二象限。解决该试题的关键是利用复数的乘法法则求出z2,根据复数的几何意义求出z2对应的点的坐标,根据坐标判断出点所在的象限.

练习册系列答案
相关题目
 (
( 为虚数单位) ,则
为虚数单位) ,则 =( )
=( )



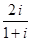 等于
等于




 ,
, 是实数,求
是实数,求 的值;
的值;  =2i,则z对应的点位于第________象限.
=2i,则z对应的点位于第________象限. ,
,  对应的点分别为
对应的点分别为 、
、 .若
.若 为线段
为线段 的中点,则点
的中点,则点



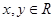 ,
,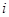 为虚数单位,且
为虚数单位,且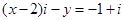 ,则
,则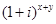 的值为( )
的值为( ) 的共轭复数为( )
的共轭复数为( )

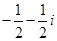

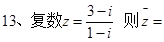 ________.
________.