题目内容
如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,A(-2,0),C(a,0)(a>0).设△AOB和△COD的外接圆圆心分别为M,N.(1)若⊙M与直线CD相切,求直线CD的方程;
(2)若直线AB截⊙N所得弦长为4,求⊙N的标准方程;
(3)是否存在这样的⊙N,使得⊙N上有且只有三个点到直线AB的距离为
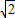 ?若存在,求此时⊙N的标准方程;若不存在,说明理由.
?若存在,求此时⊙N的标准方程;若不存在,说明理由.
【答案】分析:(1)根据△AOB为等腰直角三角形,A点坐标为(-2,0),可得圆心M的坐标为(-1,1)及圆M方程,利用⊙M与直线CD相切,圆心M到直线CD的距离等于半径,即可确定确定直线CD的方程;
(2)由已知得,直线AB的方程为x-y+2=0,圆心N的坐标为(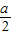 ,
,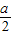 ),求出圆心N到直线AB的距离,利用直线AB截⊙N所得的弦长为4,即可确定圆心坐标,从而确定⊙N的标准方程;
),求出圆心N到直线AB的距离,利用直线AB截⊙N所得的弦长为4,即可确定圆心坐标,从而确定⊙N的标准方程;
(3)存在.由(2)知,圆心N到直线AB的距离恒为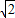 ,且AB⊥CD始终成立,当且仅当圆N的半径
,且AB⊥CD始终成立,当且仅当圆N的半径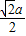 =2
=2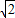 .
.
解答:解:(1)∵△AOB为等腰直角三角形,A点坐标为(-2,0),
∴圆心M的坐标为(-1,1).
∴圆M方程为(x+1)2+(y-1)2=2,
又△COD为等腰直角三角形,C点坐标为(a,0),
∴直线CD的方程为x+y-a=0
∵⊙M与直线CD相切,∴圆心M到直线CD的距离d=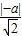 =
=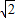 ,解得a=2或a=-2(舍).(4分)
,解得a=2或a=-2(舍).(4分)
(2)由已知得,直线AB的方程为x-y+2=0,圆心N的坐标为(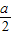 ,
,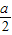 ).
).
∴圆心N到直线AB的距离为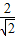 =
=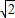 .
.
∵直线AB截⊙N所得的弦长为4,∴22+(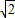 )2=
)2=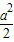 .
.
解得a=2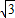 或a=-2
或a=-2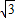 (舍),
(舍),
∴⊙N的标准方程为(x-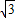 )2+(y-
)2+(y-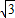 )2=6.(8分)
)2=6.(8分)
(3)存在.
由(2)知,圆心N到直线AB的距离恒为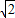 ,且AB⊥CD始终成立,
,且AB⊥CD始终成立,
∴当且仅当圆N的半径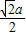 =2
=2 ,即a=4时,⊙N上有且只有三个点到直线AB的距离为
,即a=4时,⊙N上有且只有三个点到直线AB的距离为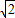 .
.
此时⊙N的标准方程为(x-2)2+(y-2)2=8.(12分)
点评:本题考查直线与圆的方程,考查直线与圆的位置关系,考查存在性问题,解题时应充分运用圆的性质,选择正确的方法.
(2)由已知得,直线AB的方程为x-y+2=0,圆心N的坐标为(
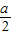 ,
,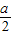 ),求出圆心N到直线AB的距离,利用直线AB截⊙N所得的弦长为4,即可确定圆心坐标,从而确定⊙N的标准方程;
),求出圆心N到直线AB的距离,利用直线AB截⊙N所得的弦长为4,即可确定圆心坐标,从而确定⊙N的标准方程;(3)存在.由(2)知,圆心N到直线AB的距离恒为
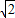 ,且AB⊥CD始终成立,当且仅当圆N的半径
,且AB⊥CD始终成立,当且仅当圆N的半径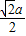 =2
=2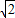 .
.解答:解:(1)∵△AOB为等腰直角三角形,A点坐标为(-2,0),
∴圆心M的坐标为(-1,1).
∴圆M方程为(x+1)2+(y-1)2=2,
又△COD为等腰直角三角形,C点坐标为(a,0),
∴直线CD的方程为x+y-a=0
∵⊙M与直线CD相切,∴圆心M到直线CD的距离d=
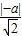 =
=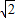 ,解得a=2或a=-2(舍).(4分)
,解得a=2或a=-2(舍).(4分)(2)由已知得,直线AB的方程为x-y+2=0,圆心N的坐标为(
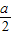 ,
,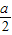 ).
).∴圆心N到直线AB的距离为
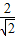 =
=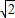 .
.∵直线AB截⊙N所得的弦长为4,∴22+(
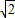 )2=
)2=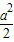 .
.解得a=2
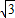 或a=-2
或a=-2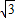 (舍),
(舍),∴⊙N的标准方程为(x-
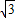 )2+(y-
)2+(y-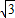 )2=6.(8分)
)2=6.(8分)(3)存在.
由(2)知,圆心N到直线AB的距离恒为
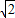 ,且AB⊥CD始终成立,
,且AB⊥CD始终成立,∴当且仅当圆N的半径
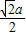 =2
=2 ,即a=4时,⊙N上有且只有三个点到直线AB的距离为
,即a=4时,⊙N上有且只有三个点到直线AB的距离为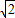 .
.此时⊙N的标准方程为(x-2)2+(y-2)2=8.(12分)
点评:本题考查直线与圆的方程,考查直线与圆的位置关系,考查存在性问题,解题时应充分运用圆的性质,选择正确的方法.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
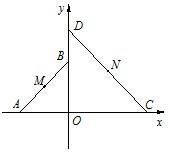 如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,A(-2,0),C(a,0),(a>0),设△AOB和△COD的
如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,A(-2,0),C(a,0),(a>0),设△AOB和△COD的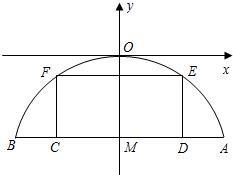 有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为8米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为8米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系. 如图,平面直角坐标系中,A(
如图,平面直角坐标系中,A( (2008•江苏二模)如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,A(-2,0),C(a,0)(a>0).设△AOB和△COD的外接圆圆心分别为M,N.
(2008•江苏二模)如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,A(-2,0),C(a,0)(a>0).设△AOB和△COD的外接圆圆心分别为M,N. (2012•虹口区二模)如图,平面直角坐标系中,射线y=x(x≥0)和y=0(x≥0)上分别依次有点A1、A2,…,An,…,和点B1,B2,…,Bn…,其中
(2012•虹口区二模)如图,平面直角坐标系中,射线y=x(x≥0)和y=0(x≥0)上分别依次有点A1、A2,…,An,…,和点B1,B2,…,Bn…,其中