题目内容
请将正确选项的序号填在横线上:
(1)函数f(x)=2-x(x>0)的反函数为f-1(x)=log2x(x>0);
(2)如果函数y=f(x)为奇函数,则f(0)=0;
(3)若f′(x0)=0,则f(x0)为极大值或极小值;
(4)随机变量ξ~N(3,12),则p(-1<ξ≤1)等于Φ(4)-Φ(2).
(1)函数f(x)=2-x(x>0)的反函数为f-1(x)=log2x(x>0);
(2)如果函数y=f(x)为奇函数,则f(0)=0;
(3)若f′(x0)=0,则f(x0)为极大值或极小值;
(4)随机变量ξ~N(3,12),则p(-1<ξ≤1)等于Φ(4)-Φ(2).
(4)
(4)
.分析:(1)函数f(x)=2-x(x>0)的反函数为f-1(x)=log
x(x>0);
(2)如果函数y=f(x)为奇函数,则f(0)=0或f(0)不存在;
(3)举出反例说明若f′(x0)=0,则f(x0)不一定为极大值或极小值;
(4)采用一般正态分布与标准正态分布的转化的方法解决,利用转化公式:P(-1<ξ≤1)=Φ(1-3)-Φ(-1-3)即可.
| 1 |
| 2 |
(2)如果函数y=f(x)为奇函数,则f(0)=0或f(0)不存在;
(3)举出反例说明若f′(x0)=0,则f(x0)不一定为极大值或极小值;
(4)采用一般正态分布与标准正态分布的转化的方法解决,利用转化公式:P(-1<ξ≤1)=Φ(1-3)-Φ(-1-3)即可.
解答:解:函数f(x)=2-x(x>0)的反函数为f-1(x)=log
x(x>0),故(1)不正确;
如果函数y=f(x)为奇函数,则f(0)=0或f(0)不存在,故(2)不正确;
若f′(x0)=0,则f(x0)不一定为极大值或极小值,
例如函数y=x3,当x=0时y′=0,但x=0不是它的极值点.故(3)不正确;
随机变量ξ~N(3,12),
则p(-1<ξ≤1)=Φ(1-3)-Φ(-1-3)=Φ(-2)-Φ(-4)=Φ(4)-Φ(2),故(4)正确.
故答案为:(4).
| 1 |
| 2 |
如果函数y=f(x)为奇函数,则f(0)=0或f(0)不存在,故(2)不正确;
若f′(x0)=0,则f(x0)不一定为极大值或极小值,
例如函数y=x3,当x=0时y′=0,但x=0不是它的极值点.故(3)不正确;
随机变量ξ~N(3,12),
则p(-1<ξ≤1)=Φ(1-3)-Φ(-1-3)=Φ(-2)-Φ(-4)=Φ(4)-Φ(2),故(4)正确.
故答案为:(4).
点评:本题考查命题真假的判断,是基础题.解题时要认真审题,仔细解答,注意反函数、奇函数、极值、正态分布等知识点的合理运用.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 的反函数为
的反函数为
 为奇函数,则
为奇函数,则
 ,则
,则 为极大值或极小值
为极大值或极小值 ~
~ ),则
),则 等于
等于 _
________
_
________ 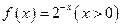 的反函数为
的反函数为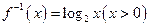
 为奇函数,则
为奇函数,则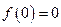
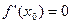 ,则
,则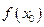 为极大值或极小值
为极大值或极小值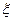 ~
~ ),则
),则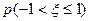 等于
等于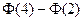 _ ________
_ ________