题目内容
已知关于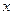 的不等式
的不等式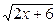
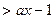 的解集为
的解集为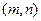 ,且
,且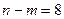 ,求
,求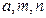 的值
的值
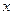 的不等式
的不等式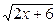
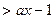 的解集为
的解集为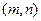 ,且
,且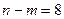 ,求
,求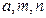 的值
的值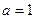 ,
,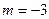 ,
,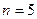
用数形结合法,如图

显然解集是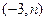 ,即
,即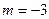 ,从而
,从而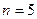
此时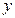 =
=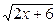 与
与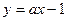 交点横坐标为5,从而纵坐标为
交点横坐标为5,从而纵坐标为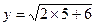
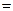 4,
4,
将交点坐标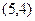 代入
代入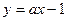 可得
可得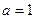
所以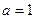 ,
,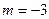 ,
,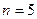

显然解集是
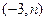 ,即
,即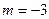 ,从而
,从而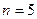
此时
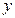 =
=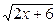 与
与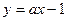 交点横坐标为5,从而纵坐标为
交点横坐标为5,从而纵坐标为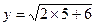
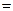 4,
4,将交点坐标
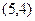 代入
代入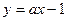 可得
可得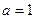
所以
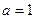 ,
,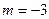 ,
,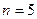

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
题目内容
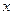 的不等式
的不等式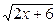
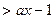 的解集为
的解集为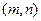 ,且
,且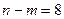 ,求
,求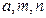 的值
的值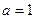 ,
,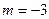 ,
,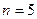

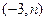 ,即
,即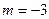 ,从而
,从而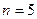
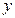 =
=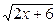 与
与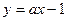 交点横坐标为5,从而纵坐标为
交点横坐标为5,从而纵坐标为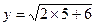
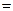 4,
4,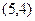 代入
代入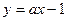 可得
可得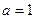
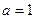 ,
,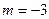 ,
,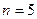

 步步高达标卷系列答案
步步高达标卷系列答案