题目内容
 如图,△OAB是边长为4的正三角形,记△OAB位于直线x=t(0<t<6)左侧的图形的面积为f(t),试求f(t)的解析式.
如图,△OAB是边长为4的正三角形,记△OAB位于直线x=t(0<t<6)左侧的图形的面积为f(t),试求f(t)的解析式.分析:根据“0<t<6”和图形,分三种情况进行讨论.
解答:解:当0<t<2时,f(t)=
•t•
t=
,
当2≤t≤4时,f(t)=
×4×2
-
(4-t)•
(4-t)=4
-8
+4
t-
t2=-
t2+4
t-4
,
当4<t<6时,f(t)=
×4×2
=4
,
所以f(t)的解析式为f(t)=
.
| 1 |
| 2 |
| 3 |
| ||
| 2 |
当2≤t≤4时,f(t)=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
当4<t<6时,f(t)=
| 1 |
| 2 |
| 3 |
| 3 |
所以f(t)的解析式为f(t)=
|
点评:本题考察分段函数解析式的求解,求解时让“直线x=t”动起来,先观察直线左侧图形是什么图形,再根据对应的面积公式来求解.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
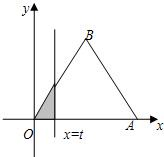 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).试求函数f(t)的解析式,并画出函数y=f(t)的图象.
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).试求函数f(t)的解析式,并画出函数y=f(t)的图象. 如图,△OAB是边长为1的等边三角形,直线x=t截这个三角形位于此直线左方的图形面积(图中阴影部分)为y,求函数y=f(t)的解析式.
如图,△OAB是边长为1的等边三角形,直线x=t截这个三角形位于此直线左方的图形面积(图中阴影部分)为y,求函数y=f(t)的解析式. 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t). (2010•武汉模拟)如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积f(t),则函数f(t)的解析式为:
(2010•武汉模拟)如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积f(t),则函数f(t)的解析式为: