题目内容
在数列
中，
，
，
．
（Ⅰ）证明：数列
是等比数列；
（Ⅱ）求数列的前
项和
；
（Ⅲ）若
对任意皆成立，求实数λ的最小值．
（Ⅰ）证明：由题设
，得
，
．
又
，所以数列
是首项为
，且公比为
的等比数列．
（Ⅱ）解：由（Ⅰ）可知
，于是数列
的通项公式为
．
所以数列的前
项和
．
（Ⅲ）由（Ⅱ）可知S1=2，S2=8，S3=27，∴
得
，
得
；
猜想实数λ的最小值为4；下面证明对任意的，
：
∵
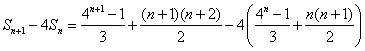
所以不等式，对任意皆成立，
∴实数λ的最小值为4．
练习册系列答案
相关题目