题目内容
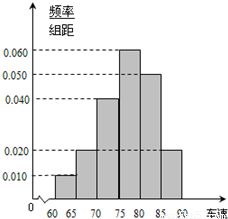
 2012年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[60,65)[65,70)[70,75)[75,80),[80,85)[85,90),得到如图的频率分布直方图.问:
2012年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[60,65)[65,70)[70,75)[75,80),[80,85)[85,90),得到如图的频率分布直方图.问:(1)某调查公司在采样中,用到的是什么抽样方法?
(2)求这40辆小型车辆车速的众数和中位数的估计值.
(3)若从车速在(60,70)的车辆中任抽取2辆,求抽出的2辆车中速车在[65,70)的车辆数ξ的分布列及其均值(即数学期望).
分析:(1)这个抽样是按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,是一个具有相同间隔的抽样,并且总体的个数比较多,这是一个系统抽样;
(2)选出直方图中最高的矩形求出其底边的中点即为众数;求出从左边开始小矩形的面积和为0.5对应的横轴的左边即为中位数;利用各个小矩形的面积乘以对应矩形的底边的中点的和为数据的平均数.
(3)从车速在(60,70)的车辆中任抽取2辆,根据题意抽出的2辆车中速车在(65,70)的车辆数ξ可能为0、1、2,求出相应的概率,即可求得分布列和期望.
(2)选出直方图中最高的矩形求出其底边的中点即为众数;求出从左边开始小矩形的面积和为0.5对应的横轴的左边即为中位数;利用各个小矩形的面积乘以对应矩形的底边的中点的和为数据的平均数.
(3)从车速在(60,70)的车辆中任抽取2辆,根据题意抽出的2辆车中速车在(65,70)的车辆数ξ可能为0、1、2,求出相应的概率,即可求得分布列和期望.
解答: 解:(1)由题意知这个抽样是按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,是一个具有相同间隔的抽样,并且总体的个数比较多,这是一个系统抽样.
解:(1)由题意知这个抽样是按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,是一个具有相同间隔的抽样,并且总体的个数比较多,这是一个系统抽样.
故调查公司在采样中,用到的是系统抽样,(2分)
(2)众数的估计值为最高的矩形的中点,即众数的估计值等于77.5 (4分)
设图中虚线所对应的车速为x,则中位数的估计值为:
0.01×5+0.02×5+0.04×5+0.06×(x-75)=0.5,
解得x=77.5,即中位数的估计值为77.5 (6分)
(3)从图中可知,车速在[60,65)的车辆数为:m1=0.01×5×40=2(辆),(7分)
车速在[65,70)的车辆数为:m2=0.02×5×40=4(辆) (8分)
∴ξ=0,1,2,
P(ξ=0)=
=
,P(ξ=1)=
=
,P(ξ=2)=
=
,
ξ的分布列为:
(11分)
数学期望Eξ=0×
+1×
+2×
=
.(12分)
 解:(1)由题意知这个抽样是按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,是一个具有相同间隔的抽样,并且总体的个数比较多,这是一个系统抽样.
解:(1)由题意知这个抽样是按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,是一个具有相同间隔的抽样,并且总体的个数比较多,这是一个系统抽样.故调查公司在采样中,用到的是系统抽样,(2分)
(2)众数的估计值为最高的矩形的中点,即众数的估计值等于77.5 (4分)
设图中虚线所对应的车速为x,则中位数的估计值为:
0.01×5+0.02×5+0.04×5+0.06×(x-75)=0.5,
解得x=77.5,即中位数的估计值为77.5 (6分)
(3)从图中可知,车速在[60,65)的车辆数为:m1=0.01×5×40=2(辆),(7分)
车速在[65,70)的车辆数为:m2=0.02×5×40=4(辆) (8分)
∴ξ=0,1,2,
P(ξ=0)=
| ||||
|
| 1 |
| 15 |
| ||||
|
| 8 |
| 15 |
| ||||
|
| 6 |
| 15 |
ξ的分布列为:
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
数学期望Eξ=0×
| 1 |
| 15 |
| 8 |
| 15 |
| 6 |
| 15 |
| 4 |
| 3 |
点评:解决频率分布直方图的有关特征数问题,利用众数是最高矩形的底边中点;中位数是左右两边的矩形的面积相等的底边的值;平均数等于各个小矩形的面积乘以对应的矩形的底边中点的和.此题把统计和概率结合在一起,比较新颖,也是高考的方向,应引起重视.

练习册系列答案
相关题目
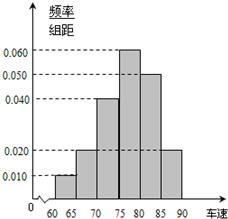
 2012年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70)[70,75),[75,80),[80,85),[85,90)后得到如图5的频率分布直方图.
2012年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70)[70,75),[75,80),[80,85),[85,90)后得到如图5的频率分布直方图.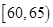 ,
,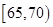 ,
, ,
,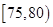 ,
,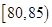 ,
,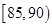 后得到如图的频率分布直方图。问:
后得到如图的频率分布直方图。问: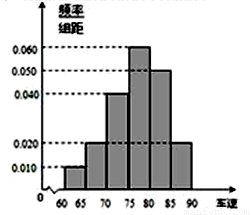
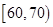 中的车辆中任取2辆,求抽出的2辆中速度在
中的车辆中任取2辆,求抽出的2辆中速度在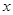 的分布列及其数学期望。(12分)
的分布列及其数学期望。(12分)