题目内容
已知半径为6的圆C与x轴相切,圆心C在直线3x+y=0上且在第二象限,直线l过点P(2,14).
(Ⅰ)求圆C的方程;
(Ⅱ)若直线l与圆C相交于A、B两点且|AB|=4
,求直线l的方程.
(Ⅰ)求圆C的方程;
(Ⅱ)若直线l与圆C相交于A、B两点且|AB|=4
| 5 |
分析:(I)设圆心,利用圆C与x轴相切则圆心到直线的距离等于半径建立等式,即可求出圆心,从而求出所求;
(II)设l的方程,利用点到直线的距离公式求出圆心到直线的距离,利用弦长的一半、半径和圆心到直线的距离构成直角三角形,建立等式,从而可求出直线方程.
(II)设l的方程,利用点到直线的距离公式求出圆心到直线的距离,利用弦长的一半、半径和圆心到直线的距离构成直角三角形,建立等式,从而可求出直线方程.
解答:解:(I)由题意,设圆心C(m,-3m)(m<0)圆C的半径r=6,
又圆C和x轴相切,则r=6=|-3m|
即m=±2,所以m=-2,所以圆C的方程为(x+2)2+(y-6)2=36
(II)设l方程为y-14=k(x-2),由d=
=
=4
∴k=
又l方程为x=2时也符合题意,故所求直线方程l的方程为x=2或3x-4y+50=0
又圆C和x轴相切,则r=6=|-3m|
即m=±2,所以m=-2,所以圆C的方程为(x+2)2+(y-6)2=36
(II)设l方程为y-14=k(x-2),由d=
| |4k-8| | ||
|
62-(2
|
∴k=
| 3 |
| 4 |
又l方程为x=2时也符合题意,故所求直线方程l的方程为x=2或3x-4y+50=0
点评:本题主要考查了直线与圆的位置关系,以及圆的方程和直线方程,同时考查了运算求解的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
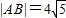 ,求直线l的方程.
,求直线l的方程.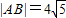 ,求直线l的方程.
,求直线l的方程.