题目内容
若向量 与向量
与向量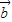 的夹角为60°,|
的夹角为60°,|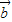 |=4,(
|=4,(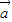 +2
+2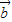 )•(
)•( -3
-3 )=-72.求:
)=-72.求:(1)|
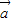 |;
|;(2)|
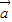 +
+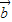 |.
|.
【答案】分析:(1)把(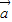 +2
+2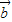 )•(
)•(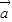 -3
-3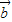 )=-72展开后化为关于|
)=-72展开后化为关于|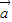 |的一元二次方程求解;
|的一元二次方程求解;
(2)利用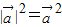 求解|
求解|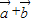 |2,则|
|2,则|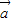 +
+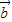 |可求.
|可求.
解答:解:(1)由(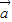 +2
+2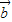 )•(
)•( -3
-3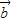 )=|
)=|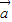 |2-|
|2-|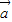 ||
||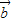 |cos 60°-6|
|cos 60°-6|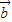 |2=|
|2=|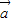 |2-2|
|2-2|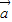 |-96=-72,
|-96=-72,
即|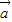 |2-2|
|2-2|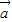 |-24=0,得|
|-24=0,得| |=6;
|=6;
(2)| |2=
|2=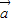 2+2
2+2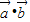 +
+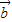 2
2
=36+2•6•4• +6=76.
+6=76.
∴| |=2
|=2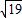 .
.
点评:本题考查了平面向量数量积的坐标表示,考查了向量的模及夹角,是基础的运算题.
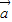 +2
+2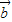 )•(
)•(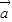 -3
-3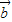 )=-72展开后化为关于|
)=-72展开后化为关于|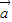 |的一元二次方程求解;
|的一元二次方程求解;(2)利用
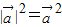 求解|
求解|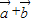 |2,则|
|2,则|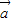 +
+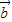 |可求.
|可求.解答:解:(1)由(
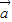 +2
+2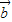 )•(
)•( -3
-3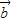 )=|
)=|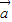 |2-|
|2-|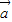 ||
||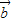 |cos 60°-6|
|cos 60°-6|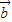 |2=|
|2=|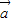 |2-2|
|2-2|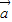 |-96=-72,
|-96=-72,即|
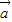 |2-2|
|2-2|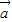 |-24=0,得|
|-24=0,得| |=6;
|=6;(2)|
 |2=
|2=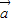 2+2
2+2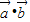 +
+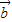 2
2=36+2•6•4•
 +6=76.
+6=76.∴|
 |=2
|=2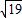 .
.点评:本题考查了平面向量数量积的坐标表示,考查了向量的模及夹角,是基础的运算题.

练习册系列答案
相关题目
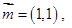 向量
向量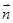 与向量
与向量 的夹角为
的夹角为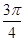 ,且
,且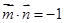 。
。 共线,向量
共线,向量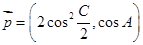 ,其中
,其中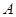 、
、 为
为 的内角,且
的内角,且 、
、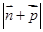 的取值范围.
的取值范围. 与向量
与向量 的夹角为60°,|
的夹角为60°,|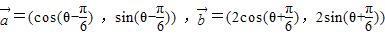 .
. 与向量
与向量 的夹角为锐角,求实数t的取值范围;
的夹角为锐角,求实数t的取值范围;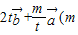 为常数,且m>0)的模的最小值.
为常数,且m>0)的模的最小值.