题目内容
设周期函数f(x)是定义在R上的奇函数,若f(x)的最小正周期为3,且f(1)>-2,f(2012)=m-
,则m的取值范围是( )
| 3 |
| m |
分析:周期函数f(x)是定义在R上的奇函数,若f(x)的最小正周期为3,可得f(2012)=f(2),求出f(2)的范围即可,f(1)=f(1-3)=f(-2)=-f(2),可得f(2)<2,求出m的范围;
解答:解:周期函数f(x)是定义在R上的奇函数,若f(x)的最小正周期为3,且f(1)>-2,
∴f(1)=f(1-3)=f(-2)=-f(2),
∴-f(2)>-2可得f(2)<2,
∴m-
<2可得
=
<0,
可得0<m<3或m<-1,
故选A;
∴f(1)=f(1-3)=f(-2)=-f(2),
∴-f(2)>-2可得f(2)<2,
∴m-
| 3 |
| m |
| m2-2m-3 |
| m |
| (m-3)(m+1) |
| m |
可得0<m<3或m<-1,
故选A;
点评:此题主要考查奇函数的性质及其应用,以及函数周期性的应用,解题的关键是能够正确求一元二次不等式,此题是一道基础题;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则m的取值范围是 .
,则m的取值范围是 . ,则m的取值范围是 .
,则m的取值范围是 .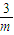 ,则m的取值范围是 .
,则m的取值范围是 .