题目内容
设虚数z1,z2,满足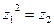 .
.
(1)若z1,z2又是一个实系数一元二次方程的两根,求z1, z2。
(2)若z1=1+mi(i为虚数单位,m∈R),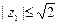 ,复数w=z2+3,求|w|的取值范围。
,复数w=z2+3,求|w|的取值范围。
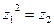 .
.(1)若z1,z2又是一个实系数一元二次方程的两根,求z1, z2。
(2)若z1=1+mi(i为虚数单位,m∈R),
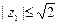 ,复数w=z2+3,求|w|的取值范围。
,复数w=z2+3,求|w|的取值范围。(1) 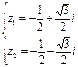 或
或 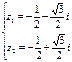 。
。
(2)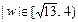 .
.
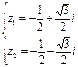 或
或 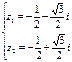 。
。(2)
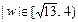 .
.(1)∵z1, z2是一个实系数一元二次方程的两个虚根,因此必共轭,
可设z1=a+bi(a,b∈R且b≠0),则z2=a-bi,
由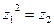 得(a+bi)2=a-bi
得(a+bi)2=a-bi
即: a2-b2+2abi=a-bi
根据复数相等,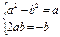
∵b≠0 解得: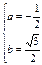 或
或 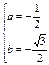 ,
,
∴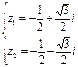 或
或 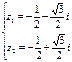 。
。
(2)由于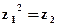 ,z1=1+mi, w=z2+3,
,z1=1+mi, w=z2+3,
∴w=(1+mi)2+3=4-m2+2mi.
∴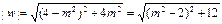 ,
,
由于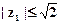 且m≠0, 可解得0<m2≤1, 令m2="u,"
且m≠0, 可解得0<m2≤1, 令m2="u," 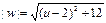 ,
,
在u∈(0,1)上,(u-2)2+12是减函数,∴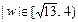 .
.
复数这一章中去掉了三角形式,降低了难度,但在复数的基本概念、运算、复数与方程、复数与几何这些部分仍然有许多可考查的内容,并且还可以与其它的数学知识相结合。
可设z1=a+bi(a,b∈R且b≠0),则z2=a-bi,
由
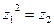 得(a+bi)2=a-bi
得(a+bi)2=a-bi即: a2-b2+2abi=a-bi
根据复数相等,
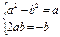
∵b≠0 解得:
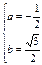 或
或 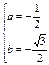 ,
,∴
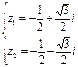 或
或 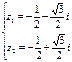 。
。(2)由于
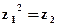 ,z1=1+mi, w=z2+3,
,z1=1+mi, w=z2+3, ∴w=(1+mi)2+3=4-m2+2mi.
∴
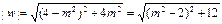 ,
,由于
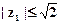 且m≠0, 可解得0<m2≤1, 令m2="u,"
且m≠0, 可解得0<m2≤1, 令m2="u," 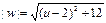 ,
,在u∈(0,1)上,(u-2)2+12是减函数,∴
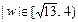 .
.复数这一章中去掉了三角形式,降低了难度,但在复数的基本概念、运算、复数与方程、复数与几何这些部分仍然有许多可考查的内容,并且还可以与其它的数学知识相结合。

练习册系列答案
相关题目
 是纯虚数,求
是纯虚数,求 在复平面内对应点的轨迹
在复平面内对应点的轨迹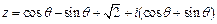 ,当
,当 为何值时,
为何值时,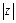 取得最大值,并求此最大值.
取得最大值,并求此最大值.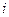 是虚数单位,
是虚数单位,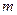 和
和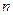 都是实数,且
都是实数,且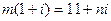 ,则
,则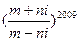 等于( )
等于( )


 ,且
,且 为正实数,则
为正实数,则 ( )
( )
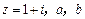 为实数.
为实数.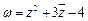 ,求
,求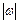 ;
;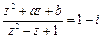 ,求
,求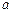 ,
,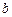 的值.
的值. 对应的点位于( ).
对应的点位于( ).
 是虚数单位
是虚数单位 的实部是 .
的实部是 . ,
, ,求证:
,求证: