题目内容
已知四棱锥的侧棱都相等,那么四棱锥的底面( )
分析:根据线面垂直的有关定理,可由侧棱长相等推出它们在底面的射影长(各条线段)相等,由此可由顶点在底面的射影为圆心,某条射影线段长为半径画圆,则底面其它顶点都在这个圆上,由此不难选出正确答案.
解答: 解:如图,四棱锥A-BCED,设顶点A在底面的射影为O
解:如图,四棱锥A-BCED,设顶点A在底面的射影为O
连接OB、OC、OE、OD,
∵AO⊥平面BCED,AB=AC=AE=AD
∴Rt△AOB≌Rt△AOC≌Rt△AOE≌Rt△AOD
∴OB=OC=OE=OD
以O为圆心,OB长为半径画圆,则C、E、D三点都在这个圆上
所以四边形BCED为圆内接四边形.
故选A.
 解:如图,四棱锥A-BCED,设顶点A在底面的射影为O
解:如图,四棱锥A-BCED,设顶点A在底面的射影为O连接OB、OC、OE、OD,
∵AO⊥平面BCED,AB=AC=AE=AD
∴Rt△AOB≌Rt△AOC≌Rt△AOE≌Rt△AOD
∴OB=OC=OE=OD
以O为圆心,OB长为半径画圆,则C、E、D三点都在这个圆上
所以四边形BCED为圆内接四边形.
故选A.
点评:本小题主要考查棱锥的结构特征、直线与平面垂直的性质等基础知识,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
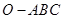 的侧棱
的侧棱 、
、 、
、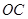 两两垂直,且
两两垂直,且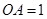 ,
,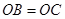
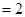 ,
, 是
是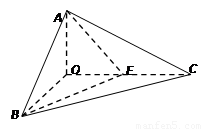
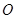 点到面
点到面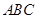 的距离;
的距离;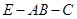 的正弦值.
的正弦值. 的侧棱长与底面边长都相等,
的侧棱长与底面边长都相等, 是
是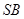 的中点,则
的中点,则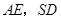 所成的角的余弦值为
( )
所成的角的余弦值为
( ) B.
B.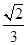 C.
C.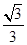 D.
D.