题目内容
在△ABC中,若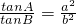 ,则△ABC的形状是
,则△ABC的形状是
- A.直角三角形
- B.等腰或直角三角形
- C.不能确定
- D.等腰三角形
B
分析:把已知等式的左边利用同角三角函数间的基本关系切化弦,右边利用正弦定理变形,然后根据二倍角的正弦函数公式化简,由A和B为三角形的内角,根据正弦函数图象与性质得到A与B角度之间的关系,根据角度之间的关系即可得到三角形ABC的形状.
解答:由正弦定理得: =
= =2R,(R为三角形外接圆的半径)
=2R,(R为三角形外接圆的半径)
∴a=2RsinA,b=2RsinB,
∴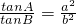 变形为:
变形为: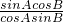 =
=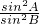 ,
,
化简得:2sinBcosB=2sinAcosA,即sin2B=sin2A,
由A和B为三角形的内角,得到2A=2B或2A+2B=180°,
即A=B或A+B=90°,
则△ABC的形状是等腰三角形或直角三角形.
故选B
点评:此题考查了正弦定理,三角函数的恒等变换及正弦函数图象与性质.根据正弦定理及同角三角函数公式化简已知的等式是本题的突破点.
分析:把已知等式的左边利用同角三角函数间的基本关系切化弦,右边利用正弦定理变形,然后根据二倍角的正弦函数公式化简,由A和B为三角形的内角,根据正弦函数图象与性质得到A与B角度之间的关系,根据角度之间的关系即可得到三角形ABC的形状.
解答:由正弦定理得:
 =
= =2R,(R为三角形外接圆的半径)
=2R,(R为三角形外接圆的半径)∴a=2RsinA,b=2RsinB,
∴
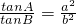 变形为:
变形为: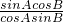 =
=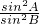 ,
,化简得:2sinBcosB=2sinAcosA,即sin2B=sin2A,
由A和B为三角形的内角,得到2A=2B或2A+2B=180°,
即A=B或A+B=90°,
则△ABC的形状是等腰三角形或直角三角形.
故选B
点评:此题考查了正弦定理,三角函数的恒等变换及正弦函数图象与性质.根据正弦定理及同角三角函数公式化简已知的等式是本题的突破点.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 ,则B的值为( )
,则B的值为( )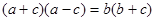 ,则∠A=( )
,则∠A=( ) B.
B. C.
C.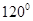 D.
D.
 ,则∠A=
,则∠A= 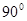 B.
B.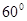 C.
C. D.
D.
 ,
, ,若
,若 ,
, ,则
,则 ()
()  A.
A. B.
B.
 D.
D.
 ,则其面积等于( )
,则其面积等于( ) B.
B. C.1
D.2
C.1
D.2