题目内容
设f(x)＝asin(πx+α)+bsin(πx+β)+4(a，b，α，β是常数)，且f(2003)＝5，则f(2004)等于
- A.1
- B.3
- C.5
- D.7
B
分析：利用诱导公式寻求f(2003)与f(2004)的关系，并注意2004π＝2003π+π的数量关系．
解：因为f(2003)＝asin(2003π+α)+b·sin(2003π+β)+4，
f(2004)＝asin(2003π+π+α)+bsin(2003π+π+β)+4
＝-asin(2003π+α)-bsin(2003π+β)+4．
所以f(2003)+f(2004)＝8．
又f(2003)＝5，所以f(2004)＝3．
故选B．
点评：要挖掘函数的特性，并结合诱导公式进行巧妙应用，使问题迎刃而解．
分析：利用诱导公式寻求f(2003)与f(2004)的关系，并注意2004π＝2003π+π的数量关系．
解：因为f(2003)＝asin(2003π+α)+b·sin(2003π+β)+4，
f(2004)＝asin(2003π+π+α)+bsin(2003π+π+β)+4
＝-asin(2003π+α)-bsin(2003π+β)+4．
所以f(2003)+f(2004)＝8．
又f(2003)＝5，所以f(2004)＝3．
故选B．
点评：要挖掘函数的特性，并结合诱导公式进行巧妙应用，使问题迎刃而解．
练习册系列答案
相关题目
)，若g(x)最大值为g(
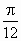)＝4，相邻的最小值点为(
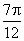，－4)且f(x)＝g(x)．
x1，x2∈R，使f(x1)－f(x2)取得最大值2时，|x1－x2|最小值为x，若f(x)在
上单调递增，在
上单调递减速，则
等于
)(A＞0，ω＞0)的图象关于直线x＝
对称，它的最小正周期是π，则f(x)图象上的一个对称中心是________(写出－个即可)．