题目内容
在下列结论中:
①函数y=sin(kπ-x)为奇函数;
②函数y=tan2x的定义域是{x∈R|x≠
+kπ,k∈z|};
③函数y=cos(2x+
)的图象的一条对称轴为x=-
π;
④方程2x-x=3的实根个数为1个.
其中正确结论的序号为
①函数y=sin(kπ-x)为奇函数;
②函数y=tan2x的定义域是{x∈R|x≠
| π |
| 2 |
③函数y=cos(2x+
| π |
| 3 |
| 2 |
| 3 |
④方程2x-x=3的实根个数为1个.
其中正确结论的序号为
①③
①③
(把所有正确结论的序号都填上).分析:利用函数的奇偶性判断①的正误;求解函数的定义域判断②的正误;利用函数的最值判断③的正误;利用函数的图象零点的个数判断④的正误.
解答:解:对于①,函数y=sin(kπ-x)=±sinx,显然函数为奇函数;①正确.
②函数y=tan2x的定义域是{x∈R|x≠
+
,k∈z|};
所以函数的定义域是{x∈R|x≠
+kπ,k∈z|}不正确;
③函数y=cos(2x+
)的图象的一条对称轴为x=-
π;因为cos[2×(-
)+
]=cos(-π)=-1,函数取得最值,所以③是正确的.
④方程2x-x=3的实根个数为1个.因为y=2x与y=x+3的图象如图:
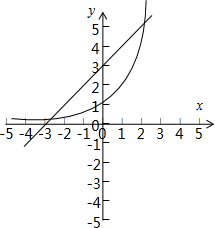 实数根的个数是2.所以判断不正确.
实数根的个数是2.所以判断不正确.
故答案为:①③.
②函数y=tan2x的定义域是{x∈R|x≠
| kπ |
| 2 |
| π |
| 2 |
所以函数的定义域是{x∈R|x≠
| π |
| 2 |
③函数y=cos(2x+
| π |
| 3 |
| 2 |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
④方程2x-x=3的实根个数为1个.因为y=2x与y=x+3的图象如图:
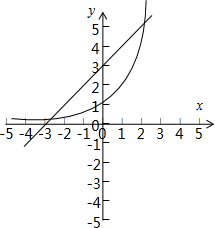 实数根的个数是2.所以判断不正确.
实数根的个数是2.所以判断不正确.故答案为:①③.
点评:本题考查函数的零点,三角函数的单调性与对称性,函数的奇偶性,基本知识的考查.

练习册系列答案
相关题目
 (k∈Z)为奇函数;
(k∈Z)为奇函数; 对称;
对称; ;
;

 为奇函数;
为奇函数; ;
; 的图象的一条对称轴为
的图象的一条对称轴为 ;
; 的实根个数为1个。 其中正确结论的序号为
的实根个数为1个。 其中正确结论的序号为