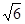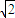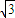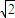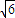题目内容
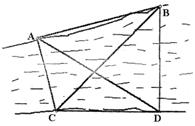
如图,要测量河对岸A、B两点间的距离,今沿河岸选取相距40米的C、D两点,测得∠ACB=60°,∠BCD=45°,∠ADB=60°,∠ADC=30°,则AB的距离为( )
A.20

B.20

C.40

D.20
【答案】分析:先根据∠ACB和∠ADB相等判断出ABCD四点共圆.根据已知求得∠BDC=90°,进而判断出BC是圆的直径.进而推断出∠CAB=90°,在Rt△BCD中,利用BC=cos45°CD求得BC,进而在Rt△ACB中,利用AC=sin30°•BC求得AC,最后根据AB=tan60°•AC求得AB的长.
解答:解:∵∠ACB和∠ADB相等.
∴ABCD四点共圆.
∴∠BDC=∠ADC+∠ADB=90°.
则BC是圆的直径.
则∠CAB=90°.
∵∠BCD=45°,∠CDB=90°,
∴BC=cos45°CD=40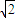
∵∠ACB=60°,∠CAB=90°,
∴AC=sin30°•BC=20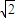 .
.
∴AB=tan60°•AC=20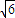
故选D.
点评:本题主要考查了解三角形的实际应用.考查了学生综合分析问题和解决实际问题的能力,属于中档题.
解答:解:∵∠ACB和∠ADB相等.
∴ABCD四点共圆.
∴∠BDC=∠ADC+∠ADB=90°.
则BC是圆的直径.
则∠CAB=90°.
∵∠BCD=45°,∠CDB=90°,
∴BC=cos45°CD=40
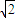
∵∠ACB=60°,∠CAB=90°,
∴AC=sin30°•BC=20
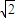 .
.∴AB=tan60°•AC=20
故选D.
点评:本题主要考查了解三角形的实际应用.考查了学生综合分析问题和解决实际问题的能力,属于中档题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
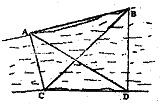 如图,要测量河对岸A、B两点间的距离,今沿河岸选取相距40米的C、D两点,测得∠ACB=60°,∠BCD=45°,∠ADB=60°,∠ADC=30°,则AB的距离为( )
如图,要测量河对岸A、B两点间的距离,今沿河岸选取相距40米的C、D两点,测得∠ACB=60°,∠BCD=45°,∠ADB=60°,∠ADC=30°,则AB的距离为( )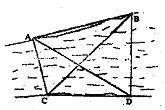
 B.20
B.20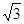 C.40
C.40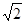 D.20
D.20