题目内容
若无穷数列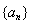 满足:①对任意
满足:①对任意 ,
, ;②存在常数
;②存在常数 ,对任意
,对任意 ,
, ,则称数列
,则称数列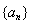 为“
为“ 数列”.
数列”.
(Ⅰ)若数列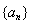 的通项为
的通项为
 ,证明:数列
,证明:数列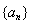 为“
为“ 数列”;
数列”;
(Ⅱ)若数列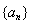 的各项均为正整数,且数列
的各项均为正整数,且数列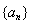 为“
为“ 数列”,证明:对任意
数列”,证明:对任意 ,
, ;
;
(Ⅲ)若数列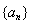 的各项均为正整数,且数列
的各项均为正整数,且数列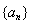 为“
为“ 数列”,证明:存在
数列”,证明:存在 ,数列
,数列 为等差数列.
为等差数列.
【答案】
(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)详见解析
【解析】
试题分析:(Ⅰ)用作差法证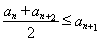 ,用单调性证
,用单调性证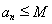 。(Ⅱ)用反证法证明。即假设存在正整数
。(Ⅱ)用反证法证明。即假设存在正整数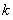 ,使得
,使得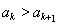 。根据
。根据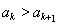 和
和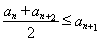 结合放缩法推倒论证得出与已知各项均为正整数相矛盾,则说明假设不成立即原命题成立。(Ⅲ)由(Ⅱ)知
结合放缩法推倒论证得出与已知各项均为正整数相矛盾,则说明假设不成立即原命题成立。(Ⅲ)由(Ⅱ)知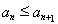 ,需分
,需分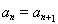 和
和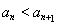 两种情况讨论,结合已知
两种情况讨论,结合已知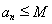 推理论证,根据等差的定义可证得存在
推理论证,根据等差的定义可证得存在 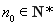 ,数列
,数列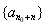 为等差数列.本题的关键是当
为等差数列.本题的关键是当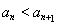 可变形得
可变形得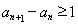 ,再用累加法表示
,再用累加法表示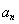 ,即
,即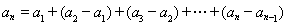 ,根据
,根据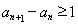 进行推理论证。
进行推理论证。
试题解析:(Ⅰ)证明:由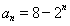 ,可得
,可得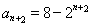 ,
,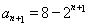 ,
,
所以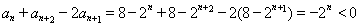 ,
,
所以对任意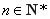 ,
,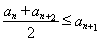 .
.
又数列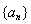 为递减数列,所以对任意
为递减数列,所以对任意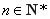 ,
,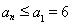 .
.
所以数列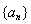 为“
为“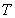 数列”. 5分
数列”. 5分
(Ⅱ)证明:假设存在正整数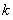 ,使得
,使得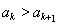 .
.
由数列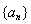 的各项均为正整数,可得
的各项均为正整数,可得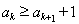 .
.
由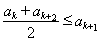 ,可得
,可得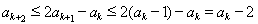 .
.
且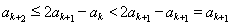 .
.
同理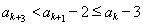 ,
,
依此类推,可得,对任意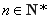 ,有
,有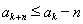 .
.
因为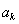 为正整数,设
为正整数,设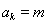 ,则
,则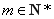 .
.
在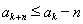 中,设
中,设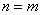 ,则
,则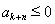 .
.
与数列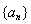 的各项均为正整数矛盾.
的各项均为正整数矛盾.
所以,对任意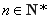 ,
,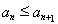 . 10分
. 10分
(Ⅲ)因为数列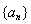 为“
为“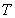 数列”,
数列”,
所以,存在常数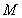 ,对任意
,对任意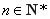 ,
,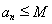 .
.
设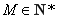 .
.
由(Ⅱ)可知,对任意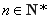 ,
,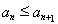 ,
,
则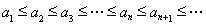 .
.
若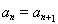 ,则
,则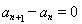 ;若
;若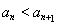 ,则
,则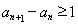 .
.
而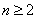 时,有
时,有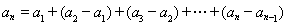 .
.
所以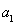 ,
,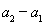 ,
,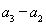 ,
,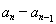 ,中最多有
,中最多有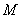 个大于或等于
个大于或等于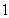 ,
,
否则与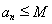 矛盾.
矛盾.
所以,存在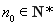 ,对任意的
,对任意的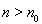 ,有
,有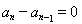 .
.
所以,对任意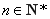 ,
,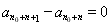 .
.
所以,存在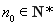 ,数列
,数列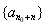 为等差数列. 14分
为等差数列. 14分
考点:新概念问题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 (1)若输入
(1)若输入