题目内容
已知锐角 满足
满足 ,则
,则 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
D
解析试题分析:由 可得
可得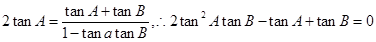 (*).因为由锐角
(*).因为由锐角 所以(*)式是一个关于
所以(*)式是一个关于 的二次方程,且存在正实根.假设存在实根韦达定理可知,两根之和为
的二次方程,且存在正实根.假设存在实根韦达定理可知,两根之和为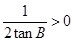 .两根之积为
.两根之积为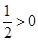 .所以只需要判别式大于或等于零.即
.所以只需要判别式大于或等于零.即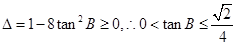 .故选D.本小题解题有一定的难度.是一道知识交汇较特殊的好题.
.故选D.本小题解题有一定的难度.是一道知识交汇较特殊的好题.
考点:1.三角函数的恒等变换.2.二次函数的根的分布.3.构造二次函数模型解决最值问题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
cos4 -sin4
-sin4 的值等于( ).
的值等于( ).
| A.0 | B. | C.1 | D. |
 =( )
=( )
| A.4 | B.2 | C. | D. |
若 ,
, 是第三象限的角,则
是第三象限的角,则 等于( )
等于( )
A. | B.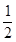 | C.-2 | D.2 |
设向量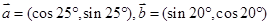 ,若
,若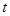 是实数,且
是实数,且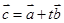 ,则
,则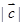 的最小值为( )
的最小值为( )
A.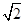 | B.1 | C. | D. |
若 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
若tanα=3, ,则tan(α﹣β)等于( )
,则tan(α﹣β)等于( )
| A.﹣3 | B. | C.3 | D. |
已知sin α=- ,且α∈
,且α∈ ,则sin 2α=( )
,则sin 2α=( )
A. | B.- | C. | D.- |
 满足
满足 ,则称
,则称 ;②
;② ;③
;③
 是
是 的内角).其中,为轮换对称式的个数是( )
的内角).其中,为轮换对称式的个数是( )


