题目内容
下列判断中错误的个数是( )
(1)命题“若q则p”与命题“若?p则?q”互为逆否命题;
(2)“am2<bm2”是“a<b”的充要条件;
(3)在△ABC中,若sinA<
,则A<
;
(4)命题“1?{1,2}或4∉{1,2}”为真命题.
(1)命题“若q则p”与命题“若?p则?q”互为逆否命题;
(2)“am2<bm2”是“a<b”的充要条件;
(3)在△ABC中,若sinA<
| 1 |
| 2 |
| π |
| 6 |
(4)命题“1?{1,2}或4∉{1,2}”为真命题.
分析:(1).命题“若p,则q”的逆否命题是“若?q,则?p”;(2).举反例即可;(3).在△ABC中,若sinA<
,则A<
或A>
;(4).只要命题p或命题q有一个命题是真命题,则p∨q为真.
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
解答:解:(1).因为命题“若p,则q”的逆否命题是命题“若?q,则?p”,所以).命题“若p,则q”与命题“若?q,则?p”互为逆否命题;故正确.
(2).错误.am2<bm2,则a<b”的逆命题为“若a<b”则am2<bm2”,令m=0,则am2=bm2,故错误.
(3).在△ABC中,若sinA<
,则A<
或A>
;故错误.
(4).命题4∉{1,2}正确,命题1?{1,2}错误,命题“1?{1,2}或4∉{1,2}”为真,故正确.
故选B.
(2).错误.am2<bm2,则a<b”的逆命题为“若a<b”则am2<bm2”,令m=0,则am2=bm2,故错误.
(3).在△ABC中,若sinA<
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
(4).命题4∉{1,2}正确,命题1?{1,2}错误,命题“1?{1,2}或4∉{1,2}”为真,故正确.
故选B.
点评:此题考查四种命题之间的真假关系,复合命题的真假关系,正弦函数的定义域和值域,属中档题.

练习册系列答案
相关题目
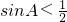 ,则
,则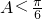 ;
;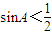 ,则
,则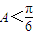 ;
;