题目内容
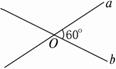
如图,直线a∥直线b,a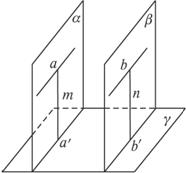
平面α，b
平面β，α⊥平γ,β⊥平面γ,a与b所确定的平面不与γ垂直.证明如果a、b不是γ的垂线，则必有α∥β．
证明：令α∩γ＝直线a′，β∩γ＝直线B′．分别过a、b上任一点在α、β内作a′、
B′的垂线m、n.根据两平面垂直的性质定理，
∵α⊥γ，β⊥γ，∴ｍ⊥γ，n⊥γ.
∴ｍ∥n．
∵a不垂直于γ，ｍ⊥γ，且a、m在α内，
∴a与m必是相交直线.
又b与n在β内，且有a∥B，ｍ∥n,
∴a∥β，ｍ∥β.∴α∥β．
讲评:根据a∥B，在α、β内另找一对平行线.由α⊥γ、β⊥γ，联想到平面垂直的性质定理.本例沟通了平行与垂直、线线与线面及面面之间的联系.
练习册系列答案
相关题目
