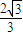题目内容
已知过点M(a,0)(a>0)的动直线l交抛物线y2=4x于A,B两点,点N与点M关于y轴对称。

(1)当a=1时,求证:∠ANM=∠BNM;
(2)对于给定的正数a,是否存在直线l':x=m,使得l'被以AM为直径的圆所截得的弦长为定值?如果存在,求出直线l'的方程;如果不存在,试说明理由。
(2)对于给定的正数a,是否存在直线l':x=m,使得l'被以AM为直径的圆所截得的弦长为定值?如果存在,求出直线l'的方程;如果不存在,试说明理由。
解:(1)设l:x-1=ny,A(x1,y1),B(x2,y2)
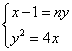 得y2-4ny-4=0,
得y2-4ny-4=0,
y1+y2=4n,y1y2=-4
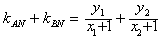
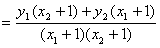
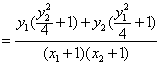 ,
,
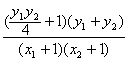
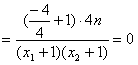
∴∠ANM=∠BNM。
(2)设点A(x,y),则以AM为直径的圆的圆心为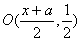 ,
,
假设满足条件的直线l存在,直线l'被圆O'截得的弦为EF,
则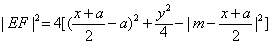
=x2-2ax+a2+4x-4m2+4m(x+a)-x2-2ax-a2
=(4m-4a+4)x+4ma-4m2
弦长|EF|为定值,则4m-4a+4=0,即m=a-1,
此时|EF|2=4m(a-m)=4(a-1),
所以当a>1时,存在直线l:x=a-1,截得的弦长为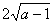
当0<a≤1时,不存在满足条件的直线l'。
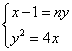 得y2-4ny-4=0,
得y2-4ny-4=0,y1+y2=4n,y1y2=-4
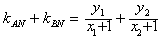
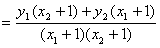
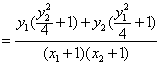 ,
,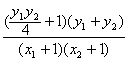
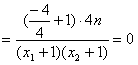
∴∠ANM=∠BNM。
(2)设点A(x,y),则以AM为直径的圆的圆心为
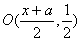 ,
,假设满足条件的直线l存在,直线l'被圆O'截得的弦为EF,
则
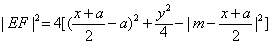
=x2-2ax+a2+4x-4m2+4m(x+a)-x2-2ax-a2
=(4m-4a+4)x+4ma-4m2
弦长|EF|为定值,则4m-4a+4=0,即m=a-1,
此时|EF|2=4m(a-m)=4(a-1),
所以当a>1时,存在直线l:x=a-1,截得的弦长为
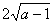
当0<a≤1时,不存在满足条件的直线l'。

练习册系列答案
相关题目
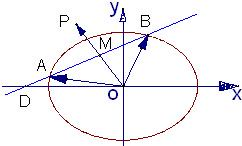 如图,已知过点D(-2,0)的直线l与椭圆
如图,已知过点D(-2,0)的直线l与椭圆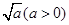 倍,求:(1)动点M的轨迹方程;(2)根据
倍,求:(1)动点M的轨迹方程;(2)根据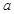 取值范围指出轨迹表示的图形.
取值范围指出轨迹表示的图形.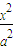 -
-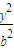 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为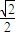 ,已知A(a,0),B(0,-b),且原点O到直线AB的距离为
,已知A(a,0),B(0,-b),且原点O到直线AB的距离为