题目内容
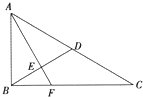 如图所示,在Rt△ABC中,∠C=30°,∠ABC=90°,D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,折起后∠AEF=θ.
如图所示,在Rt△ABC中,∠C=30°,∠ABC=90°,D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,折起后∠AEF=θ.(1)求证:平面AEF⊥平面BCD;
(2)cosθ为何值时,AB⊥CD?
分析:(1)根据折起前后没有发生变化的几何量寻找线线垂直,从而证明线面垂直,进而得到面面垂直;
(2)构造一个过直线AB且与直线CD垂直的平面,根据几何量的关系求出cosθ的值.
(2)构造一个过直线AB且与直线CD垂直的平面,根据几何量的关系求出cosθ的值.
解答:证明:(1)在Rt△ABC中,∠C=30°,D为AC的中点,则△ABD是等边三角形.
又E是BD的中点,
故BD⊥AE,BD⊥EF.
折起后,AE∩EF=E,
所以BD⊥平面AEF,而BD?平面BCD,
所以平面AEF⊥平面BCD;
(2)如图所示,
过A作AP⊥平面BCD于P,则P在FE的延长线上.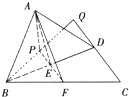
设BP与CD的延长线相交于Q,令AB=1,则△ABD是边长为1的等边三角形.
若AB⊥CD,又AP⊥CD,AB∩AP=A,则CD⊥平面ABP,于是有BQ⊥CD.
在Rt△CBQ中,∠C=30°,故∠CBQ=60°,又∠CBD=30°,故∠EBP=30°.
在Rt△EBP中,PE=BE×tan30°=
×
=
.
又AE=
,故cosAEP=
=
=
,
折起后有cosθ=cos(π-∠AEP)=-
,
故当cosθ=-
时,AB⊥CD.
又E是BD的中点,
故BD⊥AE,BD⊥EF.
折起后,AE∩EF=E,
所以BD⊥平面AEF,而BD?平面BCD,
所以平面AEF⊥平面BCD;
(2)如图所示,
过A作AP⊥平面BCD于P,则P在FE的延长线上.

设BP与CD的延长线相交于Q,令AB=1,则△ABD是边长为1的等边三角形.
若AB⊥CD,又AP⊥CD,AB∩AP=A,则CD⊥平面ABP,于是有BQ⊥CD.
在Rt△CBQ中,∠C=30°,故∠CBQ=60°,又∠CBD=30°,故∠EBP=30°.
在Rt△EBP中,PE=BE×tan30°=
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
又AE=
| ||
| 2 |
| PE |
| AE |
| ||||
|
| 1 |
| 3 |
折起后有cosθ=cos(π-∠AEP)=-
| 1 |
| 3 |
故当cosθ=-
| 1 |
| 3 |
点评:本题考查平面与平面垂直的判定,考查直线与平面垂直的性质,考查推理证明与计算能力,属于中档题.

练习册系列答案
相关题目
 22、如图所示,在Rt△ABCD中,∠ACB=90°,点O为三角形外的一点,以O为圆心,OC为半径的圆与边AB相切,切点为E,圆O与边BC相交于D点,直径EF与边BC交于G点,连接AC.
22、如图所示,在Rt△ABCD中,∠ACB=90°,点O为三角形外的一点,以O为圆心,OC为半径的圆与边AB相切,切点为E,圆O与边BC相交于D点,直径EF与边BC交于G点,连接AC. 如图所示,在Rt△ABC内有一内接正方形,它的一条边在斜边BC上,设AB=a,∠ABC=θ
如图所示,在Rt△ABC内有一内接正方形,它的一条边在斜边BC上,设AB=a,∠ABC=θ 如图所示,在Rt△ABC中,∠CAB=90°,AB=2,AC=
如图所示,在Rt△ABC中,∠CAB=90°,AB=2,AC=
 如图所示,在Rt△ABCD中,∠ACB=90°,点O为三角形外的一点,以O为圆心,OC为半径的圆与边AB相切,切点为E,圆O与边BC相交于D点,直径EF与边BC交于G点,连接AC.
如图所示,在Rt△ABCD中,∠ACB=90°,点O为三角形外的一点,以O为圆心,OC为半径的圆与边AB相切,切点为E,圆O与边BC相交于D点,直径EF与边BC交于G点,连接AC.