题目内容
设集合A={x||4x-1|≥9,x∈R},B={x|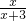 ≥0,x∈R},则A∩B=
≥0,x∈R},则A∩B=
- A.(-3,-2]
- B.(-3,-2]∪
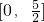
- C.(-∞,-3]∪
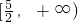
- D.(-∞,-3)∪
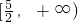
D
分析:分别求出集合A中的绝对值不等式和集合B中的其他不等式的解集,然后把两个解集表示在数轴上,即可得到两集合的交集.
解答:集合A中的不等式为|4x-1|≥9,即4x-1≥9或4x-1≤-9,解得x≥ 或x≤-2;
或x≤-2;
集合B中的不等式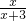 ≥0可化为
≥0可化为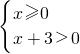 或
或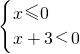 ,解得x≥0或x<-3.
,解得x≥0或x<-3.
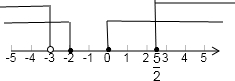
把两集合的解集表示在数轴上,如图可得A∩B=(-∞,-3)∪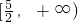
故选D
点评:本题属于以绝对值不等式和其他不等式的解法为平台,求集合交集的基础题,也是高考常考的题型.
分析:分别求出集合A中的绝对值不等式和集合B中的其他不等式的解集,然后把两个解集表示在数轴上,即可得到两集合的交集.
解答:集合A中的不等式为|4x-1|≥9,即4x-1≥9或4x-1≤-9,解得x≥
 或x≤-2;
或x≤-2;集合B中的不等式
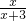 ≥0可化为
≥0可化为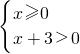 或
或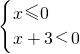 ,解得x≥0或x<-3.
,解得x≥0或x<-3.
把两集合的解集表示在数轴上,如图可得A∩B=(-∞,-3)∪
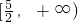
故选D
点评:本题属于以绝对值不等式和其他不等式的解法为平台,求集合交集的基础题,也是高考常考的题型.

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目