题目内容
(1) (2)
(2)
解析试题分析:解:(1) 对于
对于 ,
, 又
又 ,
, (2)由
(2)由 ,由正弦定理得
,由正弦定理得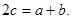
 ,即
,即 由余弦弦定理
由余弦弦定理 ,
,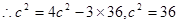 ,
,
考点:余弦定理
点评:主要是考查了向量的数量积以及余弦定理的运用,属于基础题。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
题目内容
(1) (2)
(2)
解析试题分析:解:(1) 对于
对于 ,
, 又
又 ,
, (2)由
(2)由 ,由正弦定理得
,由正弦定理得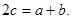
 ,即
,即 由余弦弦定理
由余弦弦定理 ,
,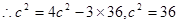 ,
,
考点:余弦定理
点评:主要是考查了向量的数量积以及余弦定理的运用,属于基础题。

 53随堂测系列答案
53随堂测系列答案