题目内容
某同学从家里到学校，为了不迟到，先跑，跑累了再走余下的路，设在途中花的时间为
，离开家里的路程为
，下面图象中，能反映该同学的情况的是（ ）
C
解析
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
已知函数
为奇函数，则
（ ）
A． | B． | C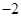． | D． |
下列函数中是奇函数的是（ ）
A． | B． | C． | D． |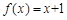
已知函数f(x)的定义域为[－3，＋∞)，且f(6)＝2。f′(x)为f(x)的导函数，f′(x)的图象如图所示．若正数a，b满足f(2a＋b)<2，则
的取值范围是( )
A． ∪(3，＋∞) | B． |
C． ∪(3，＋∞) | D． |
已知函数y=
的最大值为M,最小值为m,则
的值为 （ ）
A． | B． | C． | D． |
函数
的定义域为（ ）
A． | B． |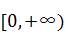
C． | D． |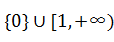
函数
的一个零点落在下列哪个区间 （ ）
| A．（0，1） | B．（1，2） | C．（2，3） | D．（3，4） |
函数
的单调递减区间是（ ）
A． | B． |
C． | D． |
下列四个函数中,在(0,+∞)上为增函数的是（ ）
A．f(x)=  | B．f(x)=x2-3x |
C．f(x)=  | D．f(x)= |