题目内容
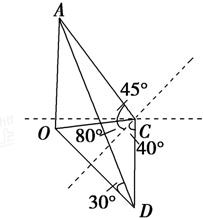某人在C点测得塔顶A为南偏西80°，仰角为45°，此人沿南偏东40°方向前进10米到D，测得塔顶A的仰角为30°，则塔高为（ ）| A、15米 | B、5米 | C、10米 | D、12米 |
分析：先设出塔高为h，进而在Rt△AOC中求得OC=OA，在Rt△AOD中根据∠ADO=30°表示出OD最后在△OCD中，利用余弦定理求得关于h的一元二次方程进而求得h．
解答：解：如图，设塔高为h，
在Rt△AOC中，∠ACO=45°，
则OC=OA=h．
在Rt△AOD中，
∠ADO=30°，则OD=
h，
在△OCD中，
∠OCD=120°，CD=10，
由余弦定理得：OD2=OC2+CD2-2OC•CDcos∠OCD，
即（
h）2=h2+102-2h×10×cos120°，
∴h2-5h-50=0，解得h=10或h=-5（舍）．
故选C
在Rt△AOC中，∠ACO=45°，
则OC=OA=h．
在Rt△AOD中，
∠ADO=30°，则OD=
| 3 |
在△OCD中，
∠OCD=120°，CD=10，
由余弦定理得：OD2=OC2+CD2-2OC•CDcos∠OCD，
即（
| 3 |
∴h2-5h-50=0，解得h=10或h=-5（舍）．
故选C
点评：本题主要考查了解三角形的实际应用．考查了学生综合分析问题和解决问题的能力．
练习册系列答案
相关题目
某人在C点测得塔顶A为南偏西80°，仰角为45°，此人沿南偏东40°方向前进10米到D，测得塔顶A的仰角为30°，则塔高为
