题目内容
已知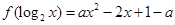 ,
,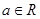 .
.
(1)求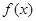 的解析式;
的解析式;
(2)解关于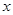 的方程
的方程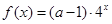
(3)设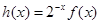 ,
,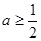 时,对任意
时,对任意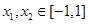 总有
总有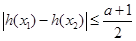 成立,求
成立,求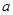 的取值范围.
的取值范围.
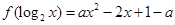 ,
,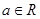 .
.(1)求
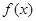 的解析式;
的解析式;(2)解关于
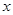 的方程
的方程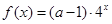
(3)设
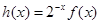 ,
,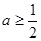 时,对任意
时,对任意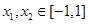 总有
总有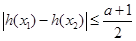 成立,求
成立,求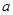 的取值范围.
的取值范围.(1)
(2)当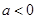 时,方程无解
时,方程无解
当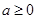 时,解得
时,解得
若 ,则
,则
若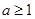 ,则
,则
(3)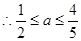

(2)当
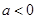 时,方程无解
时,方程无解当
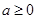 时,解得
时,解得
若
 ,则
,则
若
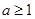 ,则
,则
(3)
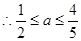
试题分析:
(1)利用换元法求解函数的解析式,设
 ,则
,则 ,代入即得
,代入即得 解析式
解析式(2)依题意将方程
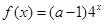 中化简得
中化简得 ,然后分
,然后分 和
和 分别求解,
分别求解,(3)对任意
 总有
总有 成立,等价于当
成立,等价于当 时,
时,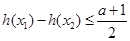 ,然后分
,然后分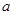 的取值来讨论.
的取值来讨论.试题解析:解:(1)令
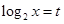 即
即 ,则
,则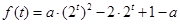
即

(2)由
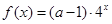 化简得:
化简得: 即
即
当
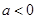 时,方程无解
时,方程无解当
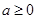 时,解得
时,解得
若
 ,则
,则
若
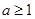 ,则
,则
(3)对任意
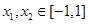 总有
总有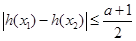 成立,等价于
成立,等价于当
 时,
时,

令
 则
则
令
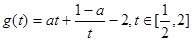
①当
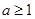 时,
时,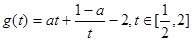 单调递增,
单调递增,此时

 ,
, 即
即 (舍)
(舍)②当
 时,
时,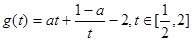 单调递增
单调递增此时

 ,
, 即
即
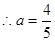
③当
 时,
时,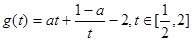
在
 上单调递减,在
上单调递减,在 上单调递增
上单调递增且
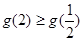


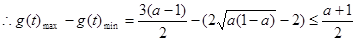 即
即
 ,综上:
,综上: 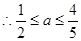

练习册系列答案
相关题目
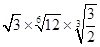 ; (2)
; (2)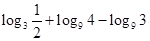 .
.
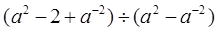
 ,若对任意的
,若对任意的 ,存在
,存在 ,使
,使 ,则实数m的取值范围是 ( )
,则实数m的取值范围是 ( )



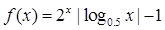 的零点个数为
的零点个数为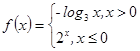 ,则
,则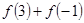 = .
= .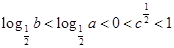 ,则 ( )
,则 ( )




 ,则
,则 ( )
( )



 ,且
,且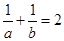 ,则
,则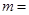 _________.
_________.