题目内容
若函数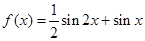 ,则
,则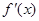 是( )
是( )
A.仅有最小值的奇函数 B. 仅有最大值的偶函数
C.既有最大值又有最小值的偶函数 D.非奇非偶函数
【答案】
C
【解析】
试题分析:由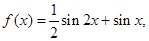 得
得 .所以
.所以 是偶函数,最大值是2,最小值是
是偶函数,最大值是2,最小值是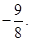
考点:正弦函数的导数,函数的奇偶性,三角函数的最值.
点评:先求出f(x)的导函数,再利用奇偶性的定义:f(-x)=f(x)或f(-x)=-f(x)判断出是奇函数还是偶函数.
因为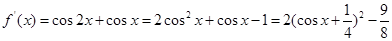 ,所以可转化为关于cosx的二次函数来求其最值,要注意cosx的取值范围为[-1,1].
,所以可转化为关于cosx的二次函数来求其最值,要注意cosx的取值范围为[-1,1].

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目