题目内容
已知O为△ABC内一点，D为BC中点，且
+
+
=0，则
=
．
| OA |
| OB |
| OC |
| OA |
-2
-2
| OD |
分析：由题意推出2
=
+
，利用向量转化，结合已知条件，求出结果．
| AD |
| AB |
| AC |
解答：解：因为△ABC内，D为BC中点，所以2
=
+
，
所以2
-2
=
-
+
-
，
所以2
=
+
，
又
+
+
=0，
所以2
=
+
=-
，
所以
=-2
．
故答案为：-2．
| AD |
| AB |
| AC |
所以2
| OD |
| OA |
| OB |
| OA |
| OC |
| OA |
所以2
| OD |
| OB |
| OC |
又
| OA |
| OB |
| OC |
所以2
| OD |
| OB |
| OC |
| OA |
所以
| OA |
| OD |
故答案为：-2．
点评：本题考查向量在几何中的应用，向量的加减法以及平行四边形法则的应用，考查转化思想与计算能力．
练习册系列答案
相关题目
已知O为平面内一定点，设条件p：动点M满足
=
+λ（
+
），λ∈R；条件q：点M的轨迹通过△ABC的重心．则条件p是条件q的（ ）
| OM |
| OA |
| AB |
| AC |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
，λ∈R；条件q：点P的轨迹通过△ABC的重心．则条件p是条件q的
=
+λ（
+
），λ∈R；条件q：点M的轨迹通过△ABC的重心．则条件p是条件q的
=
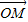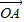+λ（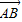
+
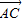），λ∈R；条件q：点M的轨迹通过△ABC的重心．则条件p是条件q的（ ）