题目内容
如图所示,在四棱锥P―ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB于点F.
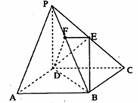
(1)证明:PA∥平面EDB;
(2)证明:PB⊥平面EFD;
(3)求DB与平面PBC所成的角.
(1)证明:连结AC交BD于O,连结OE.
∵四边形ABCD是正方形,
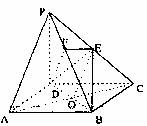
∴O为AC的中点,
∵E为PC的中点,
∴OE∥PA,
∴PA∥平面EDB.
(2)证明:∵PD⊥底面ABCD,∴PD⊥BC,
∵四边形ABCD是正方形,
∴BC⊥CD,∵BC⊥平面PCD,∵PD=DC.
∴DE⊥PC,∵DE⊥平面PBC,∴DE⊥PB,∵EF⊥PB,PB⊥平面EFD.
(3)∵DE⊥平面PBC,∠DBE就是DB与平面PBC所成的角.
设PD=DC=a,则:
在Rt△BDE中,![]() ,
,
![]()
即:DB与平面PBC所成的角为30°.

练习册系列答案
相关题目
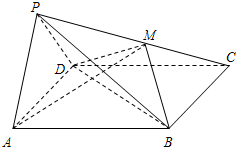 如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.
如图所示,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA∥平面BDM.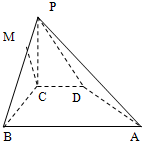 如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.
如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角. (2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
(2012•广东)如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE. 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点.
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是正方形,PD⊥平面ABCD,E为PC的中点. 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=2AB=2,M为PD上的点,若PD⊥平面MAB