题目内容
已知中心在原点，对称轴为坐标轴的双曲线的一条渐近线为y=| 4 | 3 |
分析：由渐近线方程可设a=3k，b=4k （k＞0），c=5k，由此可求出则双曲线的离心率．
解答：解：①当双曲线的焦点在x轴上时
由渐近线方程可令a=3k，b=4k （k＞0），
则c=5k，e=
．
②当双曲线的焦点在y轴上时，b=3k，a=4k （k＞0），
则c=5k，e=
．
故答案为：
或
由渐近线方程可令a=3k，b=4k （k＞0），
则c=5k，e=
| 5 |
| 3 |
②当双曲线的焦点在y轴上时，b=3k，a=4k （k＞0），
则c=5k，e=
| 5 |
| 4 |
故答案为：
| 5 |
| 3 |
| 5 |
| 4 |
点评：本题考查双曲线的离心率的性质和应用，解题时要注意公式的合理运用．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
已知中心在原点、焦点在x轴上椭圆，离心率为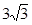
，
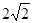），且它的左焦点F1将长轴分成2∶1，F2是椭圆的右焦点．
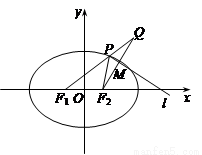（1）求椭圆的标准方程；
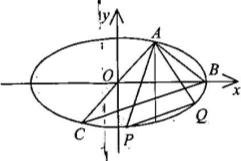已知中心在原点、焦点在x轴上椭圆，离心率为
，且过点A（1，1）
．
．
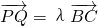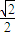，求△MAC的内切圆方程．