题目内容
设x,y满足,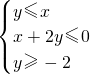 则S=x2+y2-6x+6y+18的最大值是
则S=x2+y2-6x+6y+18的最大值是
- A.17
- B.20
- C.26
- D.30
C
分析:首先根据题意做出可行域,化简S可得其几何意义为可行域中的点到(-3,3)距离的平方,分析图象可找到可行域内中距离(3,-3)最远的点,代入计算可得答案.
解答: 解:如图可行域为阴影部分,
解:如图可行域为阴影部分,
s为可行域内点到(3,-3)的距离的平方,
距离(3,-3)最远点为A(-2,-2)点,
代入s=4+4+12-12+18=26,
所以s最大值为26.
点评:本题考查线性规划可行域画法及目标函数的几何意义 较难 目标函数是个圆
分析:首先根据题意做出可行域,化简S可得其几何意义为可行域中的点到(-3,3)距离的平方,分析图象可找到可行域内中距离(3,-3)最远的点,代入计算可得答案.
解答:
 解:如图可行域为阴影部分,
解:如图可行域为阴影部分,s为可行域内点到(3,-3)的距离的平方,
距离(3,-3)最远点为A(-2,-2)点,
代入s=4+4+12-12+18=26,
所以s最大值为26.
点评:本题考查线性规划可行域画法及目标函数的几何意义 较难 目标函数是个圆

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设x,y满足,
则S=x2+y2-6x+6y+18的最大值是( )
|
| A、17 | B、20 | C、26 | D、30 |
 ,则S=x2+y2-6x+6y+18的最大值是
,则S=x2+y2-6x+6y+18的最大值是 则S=x2+y2-6x+6y+18的最大值是( )
则S=x2+y2-6x+6y+18的最大值是( )